In the previous section, we saw the two conditions which can be used to check continuity at any given point.
• In the solved examples that we saw in the previous section, we were checking the continuity at specified points like x = 0, x = 1 etc.,
•
Now let us see some examples where the given functions are continuous at every point.
Solved example 21.5
Check the points where the constant function f(x) = k is continuous.
Solution:
1. Consider any arbitrary point c. Let us check whether the function is continuous at c.
2. Applying condition (i):
•
Limiting value of f(x) at x = c is: k
•
It is clear that, $\lim_{x\rightarrow c} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(c) = k
•
We see that: $\lim_{x\rightarrow c} f(x)~=~f(c)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at x = c.
5. c was taken as an arbitrary point. So it can be any real number.
•
Therefore we can write:
The given function is continuous at every real number.
Solved example 21.6
Prove that the identity function on real numbers given by f(x) = x is continuous at every real number.
Solution:
1. Consider any arbitrary point c. Let us check whether the function is continuous at c.
2. Applying condition (i):
•
Limiting value of f(x) at x = c is: c
•
It is clear that, $\lim_{x\rightarrow c} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(c) = c
•
We see that: $\lim_{x\rightarrow c} f(x)~=~f(c)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at x = c.
5. c was taken as an arbitrary point. So it can be any real number.
•
Therefore we can write:
The given function is continuous at every real number.
•
In the above two solved examples 21.5 and 21.6, we see that, the given
functions are continuous at every point. We say that, such functions are
continuous functions. For such functions, there is no need to check for continuity at various individual points.
•
We can write the definition for continuous functions:
A real function f is said to be a continuous function, if it is continuous at every point in the domain of f.
Now we will see a special case. It can be written in steps:
1. In the solved examples 21.5 and 21.6, the domain is (−∞,∞). The functions are continuous between −∞ and ∞.
2. Let us see the case where domain is restricted. In fig.21.2 below, we see that, the domain is [a,b].
 |
| Fig.21.2 |
3. In the above fig., If the function f is to be a continuous function, then:
♦ f must be continuous at A.
♦ f must be continuous at B.
♦ f must be continuous at all the infinite points in between A and B.
4. If f is to be continuous at A, $\lim_{x\rightarrow a^{-}} f(x)$ should be equal to $\lim_{x\rightarrow a^{+}} f(x)$.
•
But there is no way to find $\lim_{x\rightarrow a^{-}} f(x)$. This is because, we do not know how x approaches 'a' from the left.
•
So there is no need to consider $\lim_{x\rightarrow a^{-}} f(x)$.
•
To check the continuity at A, we need to check only one condition: $\lim_{x\rightarrow a^{+}} f(x) ~=~f(a)$
5. Similarly, if f is to be continuous at B, $\lim_{x\rightarrow b^{-}} f(x)$ should be equal to $\lim_{x\rightarrow b^{+}} f(x)$.
•
But there is no way to find $\lim_{x\rightarrow b^{+}} f(x)$. This is
because, we do not know how x approaches 'b' from the right.
•
So there is
no need to consider $\lim_{x\rightarrow b^{+}} f(x)$.
•
To check the continuity at B, we need to check only one condition: $\lim_{x\rightarrow b^{-}} f(x) ~=~f(b)$
6. Now consider the case when the domain of f is a singleton. That is., the domain is a set which contains only one point.
•
Then the graph will be a point. We cannot check left side limit or right side limit.
•
In such a situation, we say that, f is a continuous function.
Let us see some solved examples:
Solved example 21.7
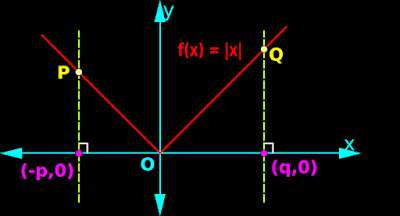
Is the function defined by f(x) = |x|, a continuous function?
Solution:
•
Fig.21.3 below shows the graph of the function f(x) = |x|.
 |
| Fig.21.3 |
Case 1: continuity of the left segment.
1. Consider any arbitrary point P on the left segment. Let us check whether the function is continuous at P.
2. Applying condition (i):
•
Limiting value of f(x) at x = -p is: p
•
It is clear that, $\lim_{x\rightarrow -p} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(-p) = |-p| = p
•
We see that: $\lim_{x\rightarrow -p} f(x)~=~f(-p)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at P.
5. P was taken as an arbitrary point. So '-p' can be any real number less than zero.
•
Therefore we can write:
The given function is continuous at every real number less than zero.
Case 2: continuity of the right segment.
1. Consider any arbitrary point Q on the right segment. Let us check whether the function is continuous at Q.
2. Applying condition (i):
•
Limiting value of f(x) at x = q is: q
•
It is clear that, $\lim_{x\rightarrow q} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(q) = |q| = q
•
We see that: $\lim_{x\rightarrow q} f(x)~=~f(q)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at Q.
5. Q was taken as an arbitrary point. So q can be any real number greater than or equal to zero.
•
Therefore we can write:
The given function is continuous at every real number greater than or equal to zero.
◼ Based on the results from the two cases. we can write:
The given function is continuous at all points.
Solved example 21.8
Discuss the continuity of the function defined by:
f(x) = x3 + x2 − 1.
Solution:
1. Consider any arbitrary point c. Let us check whether the function is continuous at c.
2. Applying condition (i):
•
Limiting value of f(x) at x = c is: c3 + c2 − 1
•
It is clear that, $\lim_{x\rightarrow c} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(c) = c3 + c2 − 1
•
We see that: $\lim_{x\rightarrow c} f(x)~=~f(c)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at x = c.
5. c was taken as an arbitrary point. So it can be any real number.
•
Therefore we can write:
The given function is continuous at every real number. Therefore, it is a continuous function.
Solved example 21.9
Is the function defined by $f(x) = \frac{1}{x},~x \ne 0$, a continuous function?
Solution:
•
Fig.21.4 below shows the graph of the function $f(x) = \frac{1}{x}$.
 |
| Fig.21.4 |
Case 1: continuity of the left segment.
1. Consider any arbitrary point P on the left segment. Let us check whether the function is continuous at P. (Note that, it is impossible to consider any point whose x coordinate is zero. It is specially mentioned in the question)
2. Applying condition (i):
•
Limiting value of f(x) at x = -p is: $-{\frac{1}{p}}$
•
It is clear that, $\lim_{x\rightarrow -p} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(-p) = $\frac{1}{(-p)}~=~-{\frac{1}{p}}$
•
We see that: $\lim_{x\rightarrow -p} f(x)~=~f(-p)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at P.
5. P was taken as an arbitrary point. So '-p' can be any real number less than zero.
•
Therefore we can write:
The given function is continuous at every real number less than zero. However, the real number 'zero' can not be considered.
Case 2: continuity of the right segment.
1. Consider any arbitrary point Q on the right segment. Let us check whether the function is continuous at Q.
2. Applying condition (i):
•
Limiting value of f(x) at x = q is: $\frac{1}{q}$
•
It is clear that, $\lim_{x\rightarrow q} f(x)$ exists. So first condition is satisfied.
3. Applying condition (ii):
f(q) = $\frac{1}{q}$
•
We see that: $\lim_{x\rightarrow q} f(x)~=~f(q)$
•
So second condition is also satisfied.
4. Since both conditions are satisfied, the given function is continuous at Q.
5. Q was taken as an arbitrary point. So 'q' can be any real number greater than zero.
•
Therefore we can write:
The given function is continuous at every real number greater than zero. However, the real number 'zero' can not be considered.
◼ Based on the results from the two cases. we can write:
The given function is continuous at all real numbers other than zero.
Based on the above solved example 21.9, we can discuss about the concept of infinity.
The graph is shown again in fig.21.5 below:
 |
| Fig.21.5 |
This can be written in 5 steps:
1. Two points Q1 and Q2 are marked on the right segment.
♦ Q2 is closer (horizontally) to zero than Q1.
♦ So q2 will be smaller than the q1.
2. The input x values are given in the denominator.
• So smaller the denominator, larger will be the value of the function f(x).
• So f(q2) will be larger than f(q1).
• It is clear that, as x approaches zero from the right, f(x) will become larger and larger.
3. When x approaches zero from the right, it take values like 0.1, 0.001, 0.0001, etc.,
• Let us find f(x) in such cases:
♦ When x = 0.1, f(x) = $\frac{1}{0.1} = 10$
♦ When x = 0.01, f(x) = $\frac{1}{0.01} = 100$
♦ When x = 0.001, f(x) = $\frac{1}{0.001} = 1000$
♦ When x = 0.0001, f(x) = $\frac{1}{0.0001} = 10000$
4. In the input x, we can give a million zeros after the decimal point. The resulting f(x) will be correspondingly large.
• We can make f(x) larger than the largest known number. All we need to do is to give the required number of zeros after the decimal point.
• "Larger than the largest known number" is denoted by the symbol +∞. It is read as plus infinity.
• +∞ is a concept. It is not a real number. We cannot do familiar calculations with +∞.
• For example:
♦ (+∞ + 4) gives +∞
♦ (+∞ ÷ 9) gives +∞
• We assume that:
+∞ is at the right end of the x-axis and at the top end of the y-axis.
5. So when $f(x) = \frac{1}{x}$, we can write: $\lim_{x\rightarrow 0^{+}} f(x)~=~+ \infty$
Case 2: The left segment.
This can be written in 5 steps:
1. Two points P1 and P2 are marked on the left segment.
♦ P2 is closer (horizontally) to zero than P1.
♦ So p2 will be smaller (numerically) than the p1.
2. The input x values are given in the denominator.
•
So smaller the denominator, larger will be the value of the function f(x).
•
So f(p2) will be larger (numerically) than f(p1).
•
It is clear that, as x approaches zero, f(x) will become larger and larger numerically.
3. But on the left segment, the x values are −ve.
•
If a "numerically larger value" is −ve, it is smaller in reality.
•
So we can write:
As x approaches zero from the left, f(x) will become smaller and smaller.
4. When x approaches zero, it take values like −0.1, −0.001, −0.0001, etc.,
•
Let us find f(x) in such cases:
♦ When x = −0.1, f(x) = $\frac{1}{-0.1} = -10$
♦ When x = −0.01, f(x) = $\frac{1}{-0.01} = -100$
♦ When x = −0.001, f(x) = $\frac{1}{-0.001} = -1000$
♦ When x = −0.0001, f(x) = $\frac{1}{-0.0001} = -10000$
5. In the input x, we can give a million zeros after the decimal point. The resulting f(x) will be correspondingly small.
•
We can make f(x) smaller than the smallest known number. All we need to
do is to give the required number of zeros after the decimal point.
•
"Smaller than the smallest known number" is denoted by the symbol −∞. It is read as minus infinity.
•
−∞ is a concept. It is not a real number. We cannot do familiar calculations with −∞.
•
For example:
♦ (−∞ + 4) gives −∞
♦ (−∞ ÷ 9) gives −∞
•
We assume that:
−∞ is at the left end of the x-axis and at the bottom end of the y-axis.
6. So when $f(x) = \frac{1}{x}$, we can write: $\lim_{x\rightarrow 0^{−}} f(x)~=~− \infty$
In the next section, we will see a few more solved examples.
Copyright©2024 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment