In the previous section,
we saw some basic details about matrices. In this section, we will see some solved examples. Later in this section, we will see types of matrices.
Solved example 19.1
The following table gives the number of men and women workers in four factories I, II, III and IV.
Represent the above information in the form of a 4 × 2 matrix. Interpret the element in the third row and second column.
Solution:
1. A 4 × 2 matrix has four rows and two columns.
2. In the given problem, there are four factories. So each factory will have a unique row
3. There are two sets of workers. Men and women. So each set will have a unique column.
4. Thus we get the following matrix:
$\left[\begin{array}{r}
{30} &{25} \\
{25} &{31} \\
{27} &{26} \\
{19} &{21} \\
\end{array}\right]$
5. Interpretation of element:
•
Third row belongs to the third factory.
•
Second column belongs to the women workers.
•
So this element is the number of women workers in the third factory.
Solved example 19.2
If a matrix has 8 elements, what are the possible orders it can have?
Solution:
1. The general form of the order is m × n
2. The product of m and n = Number of elements in the matrix = 8
•
Thus the possible values of m and n can be written as follows:
8 = (1 × 8) = (2 × 4) = (4 × 2) = (8 × 1)
3. So the possible orders are:
(1 × 8) ⇒ 1 row and 8 columns.
(2 × 4) ⇒ 2 rows and 4 columns.
(4 × 2) ⇒ 4 rows and 2 columns.
(8 × 1) ⇒ 8 rows and 1 column.
Solved example 19.3
Construct a 3 × 2 matrix whose elements are given by $a_{ij} = \frac{1}{2}|i - 3j|$
Solution:
1. In the 3 × 2 matrix, there will be 3 rows and two columns.
2. Elements in the first row are:
♦ $a_{11} = \frac{1}{2}|1 - 3 × 1| = \frac{1}{2}| -2| = \frac{1}{2}× 2 = 1$
♦ $a_{12} = \frac{1}{2}|1 - 3 × 2| = \frac{1}{2}| -5| = \frac{1}{2}× 5 = \frac{5}{2}$
3. Elements in the second row are:
♦ $a_{21} = \frac{1}{2}|2 - 3 × 1| = \frac{1}{2}| -1| = \frac{1}{2}× 1 = \frac{1}{2}$
♦ $a_{22} = \frac{1}{2}|2 - 3 × 2| = \frac{1}{2}| -4| = \frac{1}{2}× 4 = 2$
4. Elements in the third row are:
♦ $a_{31} = \frac{1}{2}|3 - 3 × 1| = \frac{1}{2}| 0| = \frac{1}{2}× 0 = 0$
♦ $a_{32} = \frac{1}{2}|3 - 3 × 2| = \frac{1}{2}| -3| = \frac{1}{2}× 3 = \frac{3}{2}$
5. Thus, the required matrix is:
$\left[\begin{array}{r}
{1} &{\frac{5}{2}} \\
{\frac{1}{2}} &{2} \\
{0} &{\frac{3}{2}} \\
\end{array}\right]
$
Types of Matrices
•
We have to learn about 7 types of matrices.
I. Column matrix
•
This can be written in 3 steps:
1. If a matrix has only one column, then it is called a column matrix.
•
The matrix A in fig.19.9 below is an example.
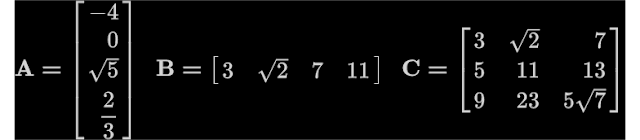 |
| Fig.19.9 |
2. The order of a column matrix will be in the form m × 1.
• So A is a 4 × 1 matrix.
3. The general form of a column matrix can be written as:
$A = \left[a_{ij} \right]_{m × 1}$
II. Row matrix
•
This can be written in 3 steps:
1. If a matrix has only one row, then it is called a row matrix.
•
The matrix B in fig.19.9 above is an example.
2. The order of a row matrix will be in the form 1 × n.
• So B is a 1 × 4 matrix.
3. The general form of a row matrix can be written as:
$B = \left[b_{ij} \right]_{1 × n}$
III. Square matrix
•
This can be written in 3 steps:
1. If, in a matrix, the number of rows is equal to the number of columns, then it is called a square matrix.
•
The matrix C in fig.19.9 above is an example.
2. The order of a row matrix will be in the form m × m.
• So C is a 4 × 4 matrix.
3. The general form of a square matrix can be written as:
$C = \left[c_{ij} \right]_{m × m}$
•
We say that, C is a square matrix of order m.
IV. Diagonal matrix
•
This can be written in 5 steps:
1. Consider any square matrix.
• We can think about a 'diagonal' from the top left element to the bottom right element.
2. All elements which lie along this diagonal, are called diagonal elements.
• All the remaining elements are called non-diagonal elements.
3. In a square matrix, if all the non-diagonal elements are zero, then it is called a diagonal matrix.
4. We can write the general form of a diagonal matrix as follows:
$D = \left[d_{ij} \right]_{m × m}$ is a diagonal matrix if dij = 0 when i ≠ j.
5. Fig.19.10 below shows some diagonal matrices.
 |
| Fig.19.10 |
• In the above fig.,
♦ A is a diagonal matrix of order 1.
♦ B is a diagonal matrix of order 2.
♦ C is a diagonal matrix of order 3.
V. Scalar matrix
•
This can be written in 3 steps:
1. Consider any diagonal matrix.
• In that diagonal matrix, if all the diagonal elements are equal, then it is called a scalar matrix.
2. We can write the general form of a scalar matrix as follows:
• A square matrix $A = \left[a_{ij} \right]_{m × m}$ is a scalar matrix if two conditions are satisfied:
♦ aij = 0 when i ≠ j.
♦ aij = k when i = j, where k is a constant.
3. Fig.19.11 below shows some scalar matrices.
 |
| Fig.19.11 |
• In the above fig.,
♦ A is a scalar matrix of order 1.
♦ B is a scalar matrix of order 2.
♦ C is a scalar matrix of order 3.
VI. Identity matrix
•
This can be written in 5 steps:
1. Consider any scalar matrix.
• In that scalar matrix, if k = 1, then it is called an identity matrix.
2. We can write the general form of an identity matrix as follows:
• A square matrix $A = \left[a_{ij} \right]_{m × m}$ is an identity matrix if two conditions are satisfied:
♦ aij = 0 when i ≠ j.
♦ aij = 1 when i = j.
3. Fig.19.12 below shows some identity matrices.
 |
| Fig.19.12 |
• In the above fig.,
♦ A is an identity matrix of order 1.
♦ B is an identity matrix of order 2.
♦ C is an identity matrix of order 3.
4. Denoting an identity matrix:
• If the order of an identity matrix is n, then we denote that matrix as In.
• So in the fig.19.12 above,
♦ A = I1.
♦ B = I2.
♦ C = I3.
• If the order is clear from the context, we simply denote it as I.
5. Note that:
• Every identity matrix, is a scalar matrix.
• But every scalar matrix need not be an identity matrix.
VII. Zero matrix
•
This can be written in 3 steps:
1. Consider any matrix (it need not be a square matrix).
• In that matrix, if all the elements are zero, then it is called a zero matrix.
2. Fig.19.13 below shows some zero matrices.
 |
| Fig.19.13 |
3. Denoting an identity matrix:
• We denote a zero matrix by O. It's order will be clear from the context.
In the next section, we will see equality of matrices.
Copyright©2024 Higher secondary mathematics.blogspot.com

No comments:
Post a Comment