19.3 - Addition of Matrices

In the previous section, we saw equality of matrices. In this section, we will see operations on matrices.

First we will see addition of matrices. It can be explained in 6 steps:
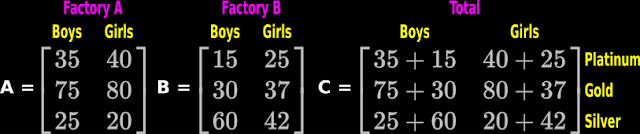
1. An industrialist has two factories. Factory A and Factory B. Both produces bicycles for boys and girls.
2. Bicycles are produced in three price tags: Platinum class, Gold class and Silver class.
◼ For example:
• Factory A produces:
   ♦ 35 Platinum class bicycles for boys and 40 Platinum class bicycles for girls.  
   ♦ 75 Gold class bicycles for boys and 80 Gold class bicycles for girls.  
   ♦ So on . . .
3. This data can be effectively represented using matrices A and B as shown in fig.19.14 below:

Fig.19.14

4. Now, if the industrialist wants to know the total production in each class, he can simply add the two matrices together. The resulting matrix C is shown in the same fig.19.14 above.
• The industrialist now know that, from the two factories,
   ♦ (35+15) = 50 platinum class is produced for boys.
   ♦ (40+25) = 65 platinum class is produced for girls.
   ♦ (75+35) = 110 Gold class is produced for boys.
   ♦ So on . . .
5. We see that, to find the sum, all we need to do, is to add the corresponding terms together.
• But it is important to make sure that, the matrices being added, are of the same order. If they are not of the same order, then the sum is not defined.
6. So we can write:
If A = [a_ij]_m×n and B = [b_ij]_m×n are two matrices of the same order m×n, then the sum of the two matrices A and B is defined as a matrix C = [c_ij]_m×n, where c_ij = a_ij + b_ij for all possible values of i and j.
• Using symbols, this is written as:
A + B = [a_ij] + [b_ij] = [a_ij + b_ij] = C

Solved example 19.7
If A = $\left[\begin{array}{r}           
4    &{\sqrt5}    &{2}    \\
6    &{0}    &{-9}    \\
\end{array}\right]$ and B = $\left[\begin{array}{r}           
\sqrt3    &{7}    &{5}    \\
-2    &{\frac{2}{3}}    &{9}    \\
\end{array}\right]           
$, then find A+B
Solution:
• Both A and B are of the same order. So addition of A and B is defined. We get:
A+B = $\left[\begin{array}{r}           
4+\sqrt3    &{\sqrt5 + 7}    &{2+5}    \\
6 – 2    &{0 + \frac{2}{3}}    &{-9+9}    \\
\end{array}\right]~=~
\left[\begin{array}{c}           
4+\sqrt3    &{\sqrt5 + 7}    &{7}    \\
4    &{\frac{2}{3}}    &{0}    \\
\end{array}\right]$

---

Properties of Matrix addition

Matrix addition satisfy the following four properties:
(i) Commutative law
(ii) Associative law
(iii) Existence of additive identity
(iv) Existence of additive inverse

(i) Commutative law
• If A = [a_ij]_m×n and B = [b_ij]_m×n are two matrices of the same order m×n, then A+B = B+A
• Proof can be written in 3 steps:
1. A + B = [a_ij] + [b_ij] = [a_ij + b_ij]
We already saw this when we discussed matrix addition.
2. a_ij and b_ij are numbers. Addition of numbers is commutative. So (1) can be modified as:
A + B = [b_ij + a_ij]
3. [b_ij + a_ij] means that, every element of B is being added to the corresponding element of A.
• So it is the addition of B and A.
• Thus (2) can be modified as: A+B = B+A

(ii) Associative law
• If A = [a_ij]_m×n , B = [b_ij]_m×n and C = [c_ij]_m×n are three matrices of the same order m×n, then (A+B)+C = A+(B+C)
• Proof can be written in 6 steps:
1. A + B = [a_ij] + [b_ij] = [a_ij + b_ij]
We already saw this when we discussed matrix addition.
2. So (A+B) + C = [a_ij + b_ij]+ [c_ij]
3. (2) can be modified by using the same procedure in (1). We get:
(A+B) + C = [a_ij + b_ij]+ [c_ij] = [(a_ij + b_ij) + c_ij]
4. a_ij , b_ij and c_ij are numbers. Addition of numbers is associative. So (3) can be modified as:
(A+B) + C = [(a_ij + b_ij) + c_ij] = [a_ij + (b_ij + c_ij)]
5. Consider the last term of the result in (4). It indicates that, two matrices are being added. The matrices being added are: A and (B+C).
• That is:
[a_ij + (b_ij + c_ij)] = [a_ij] + [(b_ij + c_ij)] = A + (B+C)
6. based on the results in (4) and (5), we get:
(A+B) + C = A + (B+C)

(iii) Existence of additive identity
• If A = [a_ij]_m×n and O = [0_ij]_m×n are two matrices of the same order m×n, then A+O = O+A = A
• Proof can be written in 4 steps:
1. A + O = [a_ij] + [0_ij] = [a_ij + 0_ij]
We already saw this when we discussed matrix addition.
• But [a_ij + 0_ij] = [a_ij] = A
• So we can write:
A + O = A
2. O + A = [0_ij] + [a_ij] = [0_ij + a_ij]
We already saw this when we discussed matrix addition.
• But [0_ij + a_ij] = [a_ij] = A
• So we can write:
O + A = A
3. Based on (1) and (2), we can write: A+O = O+A = A
4. Whenever we add O to a matrix A, the sum will be the same matrix A. So O is called the additive identity for matrix addition.

(iv) Existence of additive inverse
• If A = [a_ij]_m×n and A = [-a_ij]_m×n are two matrices of the same order m×n, then A+(-A) = (-A)+A = O
(Here, -A is a matrix obtained by multiplying each element of A by -1)
• Proof can be written in 4 steps:
1. A + (-A) = [a_ij] + [-a_ij] = [a_ij + -a_ij] = [a_ij - a_ij]
We already saw this when we discussed matrix addition.
• But [a_ij - a_ij] = [0_ij] = O
• So we can write:
A + (-A) = O
2. (-A) + A = [-a_ij] + [a_ij] = [-a_ij + a_ij]
We already saw this when we discussed matrix addition.
• But [-a_ij + a_ij] = [0_ij] = O
• So we can write:
(-A) + A = O
3. Based on (1) and (2), we can write: A+(-A) = (-A)+A = O
4. Whenever we add -A to a matrix A, the sum will be the zero matrix O. So -A is called the additive inverse of A or negative of A.

---

In the next section, we will see multiplication of a matrix by a scalar. 

Previous

Contents

Next

Copyright©2024 Higher secondary mathematics.blogspot.com