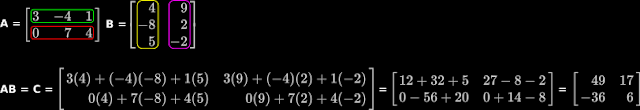In the previous section,
we completed a discussion on multiplication of matrix by a scalar. In this
section, we will see multiplication of matrices.
Multiplication of two matrices can be explained using an example. It can be written in 5 steps:
1. Consider three students: Student X, Student Y and Student Z.
• They want to buy some notebooks, pens and pencils.
♦ X requires 8 notebooks, 3 pens and 2 pencils.
♦ Y requires 7 notebooks, 5 pens and 3 pencils.
♦ Z requires 11 notebooks, 4 pens and 2 pencils.
• This is shown as the matrix A in fig.19.20 below:
 |
| Fig.19.20 |
2. The students go to a nearby store. there:
♦ Notebooks cost Rs. 25 each.
♦ Pens cost Rs. 12 each.
♦ Pencils cost Rs. 5 each.
• This is shown as the matrix B in fig.19.20 above.
3. Using the data in the matrices A and B, we can calculate the payments to be made.
• For student X,
♦ Cost of notebooks = 8 × 25
♦ Cost of pens = 3 × 12
♦ Cost of pencils = 2 × 5
• So total payment to be made by student X = (8 × 25) + (3 × 12) + (2 × 5) = 246
• This is same as: (a
11 × b
11) + (a
12 × b
21) + (a
13 × b
31) = c
11.
• The sum 246, is the element c
11 of matrix C. This is shown in fig.19.20 above.
4. In this way, we can find the payment to be made by each student. The method is shown below:
$\begin{array}{ll} {~\color{magenta} 1 } &{\text{Student X}} &{(8 × 25) + (3 × 12) + (2 × 5)} & {~=~} &{246} \\
{~\color{magenta} 2 } &{\implies} &{(a_{11} × b_{11})\,+\,(a_{12} × b_{21})\,+\,(a_{13} × b_{31})} & {~=~} &{c_{11}} \\
{~\color{magenta} 3 } &{\text{Student Y}} &{(7 × 25) + (5 × 12) + (3 × 5)} & {~=~} &{250} \\
{~\color{magenta} 4 } &{\implies} &{(a_{21} × b_{11})\,+\,(a_{22} × b_{21})\,+\,(a_{23} × b_{31})} & {~=~} &{c_{21}} \\
{~\color{magenta} 5 } &{\text{Student Z}} &{(11 × 25) + (4 × 12) + (2 × 5)} & {~=~} &{333} \\
{~\color{magenta} 6 } &{\implies} &{(a_{31} × b_{11})\,+\,(a_{32} × b_{21})\,+\,(a_{33} × b_{31})} & {~=~} &{c_{31}} \\
\end{array}$
• The reader is advised to check the above steps and recognize the neat pattern that exists between aij, bij and cij.
5. It is clear that,
♦ Each row of matrix A is multiplied by the column of matrix B.
♦ Such a multiplication and subsequent summation, gives the matrix C.
We can write: AB = C
Let us see another example. It can be written in 6 steps:
1. Consider the same three students in the previous example: Student X, Student Y and Student Z.
Their requirements are also the same. So matrix A is the same. It is shown in fig.19.21 below:
 |
| Fig.19.21 |
2. This time the students decide to check another store. So we will name the first store as I and the second store as II.
• At store II:
♦ Notebooks cost Rs. 24 each.
♦ Pens cost Rs. 14 each.
♦ Pencils cost Rs. 6 each.
• The prices at the two stores can be written together as a matrix. This is shown as the matrix D in fig.19.21 above.
3. Using the data in the matrices A and D, we can calculate the payments to be made.
• For student X,
♦ Cost of notebooks = 8 × 24
♦ Cost of pens = 3 × 14
♦ Cost of pencils = 2 × 6
• So total payment to be made by student X = (8 × 24) + (3 × 14) + (2 × 6) = 246
• This is same as: (a11 × d12) + (a12 × d22) + (a13 × d32) = e12.
• The sum 246, is the element e12 of matrix E. This is shown in fig.19.21 above.
4. In this way, we can find the payment to be made by each student. The method is shown below:
$\begin{array}{ll}
{~\color{magenta} 1 } &{\text{Student X}} &{(8 ×
24) + (3 × 14) + (2 × 6)} & {~=~} &{246} \\
{~\color{magenta}
2 } &{\implies} &{(a_{11} × d_{12})\,+\,(a_{12} ×
d_{22})\,+\,(a_{13} × d_{32})} & {~=~} &{e_{11}} \\
{~\color{magenta}
3 } &{\text{Student Y}} &{(7 × 24) + (5 × 14) + (3 ×
6)} & {~=~} &{256} \\
{~\color{magenta} 4 }
&{\implies} &{(a_{21} × d_{21})\,+\,(a_{22} ×
d_{22})\,+\,(a_{23} × d_{32})} & {~=~} &{e_{22}} \\
{~\color{magenta}
5 } &{\text{Student Z}} &{(11 × 24) + (4 × 14) + (2 ×
6)} & {~=~} &{332} \\
{~\color{magenta} 6 }
&{\implies} &{(a_{31} × d_{12})\,+\,(a_{32} ×
d_{22})\,+\,(a_{33} × d_{32})} & {~=~} &{e_{32}} \\
\end{array}$
• In this way the second column of matrix E is calculated.
• The reader is advised to check the above steps and recognize the neat pattern that exists between aij, dij and eij.
5. It is clear that,
♦ Each row of matrix A is multiplied by the second column of matrix D.
♦ Such a multiplication and subsequent summation, gives the second column of matrix E. (the first column is same as in the previous example)
We can write: AD = E
6. Now we can compare the matrix C from the first example and matrix E from the second example.
• If the students go to the store II,
♦ They will suffer a loss of Rs.6/- in the case of student Y.
♦ They will get a gain of Rs.1/- in the case of student Z.
♦ So they will suffer a net loss of Rs.5/-
Let us see one more example.
If A = $\left[\begin{array}{r}
3 &{-4} &{1} \\
0 &{7} &{4} \\
\end{array}\right]
$ and B = $\left[\begin{array}{r}
4 &{9} \\
-8 &{2} \\
5 &{-2} \\
\end{array}\right]
$, then find AB
This time, we will avoid the detailed steps:
• Multiply green rectangle by the yellow rectangle. The summation will give c11. See fig.19.22 below:
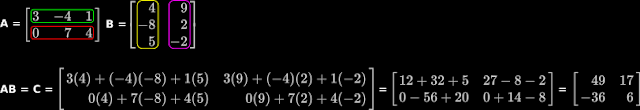 |
| Fig.19.22 |
• Multiply green rectangle by the magenta rectangle. The summation will give c
12.
• Multiply red rectangle by the yellow rectangle. The summation will give c
21.
• Multiply red rectangle by the magenta rectangle. The summation will give c
22.
Based on the three examples, we can write two important points:
1. We are given two matrices A and B.
• We will be able to calculate AB only if:
Number of columns in A = Number of rows in B
• In other words:
♦ If A is of the order (m×n),
♦ Then B must be of the order (n×p).
2. When we multiply A of order (m×n) and B of order (n×p), the order of the resulting AB will be (m×p).
Now we will see a solved example:
Solved example 19.13
Find AB if A = $\left[\begin{array}{r}
14 &{12} \\
7 &{8} \\
\end{array}\right]
$ and B = $\left[\begin{array}{r}
5 &{4} &{8} \\
9 &{7} &{3} \\
\end{array}\right]
$.
Solution:
$\begin{array}{ll} {~\color{magenta} 1 } &{{}} &{AB} & {~=~} &{\left[\begin{array}{r}�� 14�&{12}�\\ 7�&{8}�\\ \end{array}\right]�� \left[\begin{array}{r}��� 5�&{4}�&{8}�\\ 9�&{7}�&{3}�\\ \end{array}\right]��� } \\
{~\color{magenta} 2 } &{{}} &{{}} & {~=~} &{\left[\begin{array}{r}��� 14(5)+12(9)�&{14(4)+12(7)}�&{14(8)+12(3)}�\\ 7(5)+8(9)�&{7(4)+8(7)}�&{7(8)+8(3)}�\\ \end{array}\right]��� } \\
{~\color{magenta} 3 } &{{}} &{{}} & {~=~} &{\left[\begin{array}{r}��� 70+108 �&{56+84}�&{112+36}�\\ 35+72�&{28+56}�&{56+24}�\\ \end{array}\right]��� } \\
{~\color{magenta} 4 } &{{}} &{{}} & {~=~} &{\left[\begin{array}{r}��� 178 �&{140}�&{148}�\\ 107�&{84}�&{80}�\\ \end{array}\right]��� } \\
\end{array}$
Let us see some interesting facts. They can be written in 4 steps:
1. In the above solved example, we saw that, AB is possible.
• This is because:
Number of columns in A = Number of rows in B = 3.
2. Is BA possible?
♦ Number of columns in B = 3
♦ Number of rows in A = 2
• We see that:
Number of columns in B ≠ Number of rows in A.
• So it is not possible to find BA. In other words, BA is not defined.
3. So we can write:
"AB being defined", gives no guarantee that, BA is also defined.
4. What is the condition for both AB and BA to be defined?
• Answer can be written in 8 steps:
(i) Given two matrices A and B
♦ A is of the order (m×n)
♦ B is of the order (k×l)
(ii) Suppose that, AB is defined. Then n = k = u
(iii) For checking BA, we consider the orders (k×l) and (m×n).
(iv) For BA to be defined, l and m must be equal. That is., l = m = v
(v) Based of (ii) and (iv), we can write:
♦ order of A = (m×n) = (v×u)
♦ order of B = (k×l) = (u×v)
(vi) So we can write:
• If both AB and BA is to be defined, then:
Order of A must be (v×u) and that of B must be (u×v)
(that is., u and v are interchanged)
(vii) For example, A and B are of the orders (3×4) and (4×3) respectively, then both AB and BA are defined.
(viii) A particular case arises when A and B are square matrices of the same order.
• In such a situation, u will be equal to v. Then, interchanging u and v will give the same order.
• So we can write:
If A and B are two square matrices of the same order, then both AB and BA are defined.
In the next section, we will see that multiplication of matrices is not commutative.
Previous
Contents
Next
Copyright©2024 Higher secondary mathematics.blogspot.com