In the previous section, we saw the fourth and fifth properties of inverse trigonometric functions. In this section, we will see the sixth property.
Property VI
• This has 3 parts:
$\begin{array}{cc}{} &{\text{(i)}} &{2 \tan^{-1}x} &{}={} &{\sin^{-1}\frac{2x}{1+x^2}}, &{|x| \le 1}\\ {}
&{\text{(ii)}} &{2\tan^{-1}x} &{}={} &{\cos^{-1}\frac{1-x^2}{1+x^2}}, &{x \ge 0}\\ {}
&{\text{(iii)}} &{2\tan^{-1}x} &{}={} &{\tan^{-1}\frac{2x}{1-x^2}}, &{-1 < x < 1}\\ \end{array}$
• Let us prove part (i):
◼ Remarks:
• In line A, we assume that $\tan^{-1}(x)$ = y
• In line B, we use the identity 15.
♦ List of identities can be seen here.
• In line C, we substitute for y from A.
• Let us prove part (ii):
◼ Remarks:
• In line A, we assume that $\tan^{-1}(x)$ = y
• In line B, we use the identity 14.
♦ List of identities can be seen here.
• In line C, we substitute for y from A.
• Let us prove part (iii). We already saw the proof in property V. Here we will see an alternate method:
◼ Remarks:
• In line A, we assume that $\tan^{-1}(x)$ = y
• In line B, we use the identity 16.
♦ List of identities can be seen here.
• In line C, we substitute for y from A.
Now we will see some solved examples.
Solved example 18.3
Show that
$\begin{array}{cc}{} &{\text{(i)}} &{\sin^{-1} \left(2x{\sqrt{1-x^2}} \right)} &{}={} &{2\sin^{-1}x}, &{-{\frac{1}{\sqrt2}} \le x \le \frac{1}{\sqrt2}}\\ {}
&{\text{(ii)}} &{\sin^{-1} \left(2x{\sqrt{1-x^2}} \right)} &{}={} &{2\cos^{-1}x}, &{-{\frac{1}{\sqrt2}} \le x \le 1}\\ {}
\end{array}$
Solution:
Part (i):
◼ Remarks:
• Line 1: We assume that $\sin^{-1}(x)$ = y
• Line 3: We use the identity sin2𝜃 + cos2𝜃 = 1.
• Line 6: We use the identity 15.
♦ List of identities can be seen here.
• Line 8: We take the inverse.
• Line 9: We substitute for y based on the assumption in (1).
Part (ii):
◼ Remarks:
• Line 1: We assume that $\cos^{-1}(x)$ = y
• Line 3: We use the identity sin2𝜃 + cos2𝜃 = 1.
• Line 6: We use the identity 15.
♦ List of identities can be seen here.
• Line 8: We take the inverse.
• Line 9: We substitute for y based on the assumption in (1).
Solved example 18.4
Show that $\tan^{-1}\frac{1}{2} + \tan^{-1}\frac{2}{11} = \tan^{-1}\frac{3}{4}$
Solution:
◼ Remarks:
• Line 1: We use part 2 of property 5.
• Line 2: We substitute the known values.
In the next section, we
will see a few more solved examples.
Previous
Contents
Copyright©2024 Higher secondary mathematics.blogspot.com




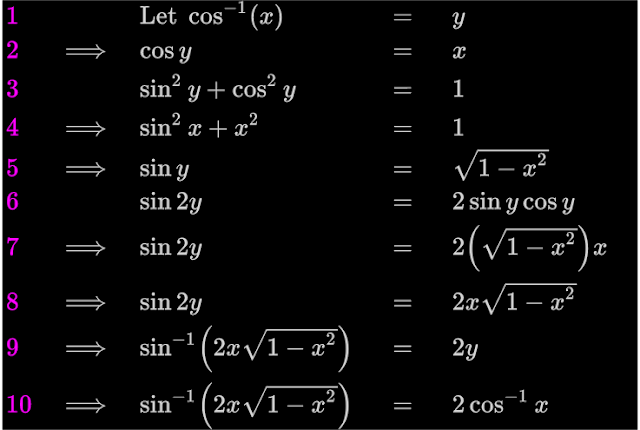

No comments:
Post a Comment