In the previous section, we completed a discussion on inverse trigonometric functions. In this section, we will see some miscellaneous examples.
Solved example 18.9
Find the value of $\sin^{-1}\left(\sin \frac{3 \pi}{5}\right)$
Solution:
• We know that, sin-1(sin x) = x. So we get $\sin^{-1}\left(\sin \frac{3 \pi}{5}\right)~=~\frac{3 \pi}{5}$
• sin-1(sin x) is a composite function. Also, we must consider the principal branch. So this composite function is a function on $\left[- \frac{\pi}{2}, \frac{\pi}{2} \right]$. That means, both input and output must be available in the set $\left[- \frac{\pi}{2}, \frac{\pi}{2} \right]$. Details can be seen here.
• In our present case, $\frac{3\pi}{5}$ is not available in the set $\left[- \frac{\pi}{2}, \frac{\pi}{2} \right]$.
• So the given expression should be simplified as follows:
◼ Remarks:
1. Use identity 9(d).
♦ List of identities can be seen here.
Solved example 18.10
Show that $\sin^{-1}\frac{3}{5} \,-\, \sin^{-1}\frac{8}{17}\,=\,\cos^{-1}\frac{84}{85}$.
Solution:
◼ Remarks:
7.Use the identity 4.
♦ List of identities can be seen here.
Solved example 18.11
Show that $\sin^{-1} \frac{12}{13} \;+\; \cos^{-1}\frac{4}{5} + \tan^{-1}\frac{63}{16} =
\pi$.
Solution:
Part (i):
The given expression can be rearranged as shown below:
◼ Remarks:
3. Instead of proving the given expression, we can prove the expression in this line.
Part (ii): Simplifying the L.H.S of part(i)
Part (iii): Simplifying the R.H.S of part(i)
◼ Remarks:
1. Use the identity 11.
List of trigonometric identities can be seen here.
2. tan π = 0
Part (iv): Comparing L.H.S and R.H.S
•
Results from parts (ii) and (iii) are the same.
•
So we can write:
L.H.S of part (i) = R.H.S of part (i)
Solved example 18.12
Simplify $\tan^{-1}\left[\frac{a \cos x\,-\, b \sin x}{b \cos x\,+\, a \sin x} \right],~\text{if}~\frac{a}{b} \tan x > -1$.
Solution:
◼ Remarks:
1. We have to calculate y.
3. Divide both numerator and denominator by b cos x.
4. Use identity 11.
♦ List of trigonometric identities can be seen here.
Solved example 18.13
Solve $\tan^{-1} 2x \,+\, \tan^{-1} 3x \,=\,\frac{\pi}{4}$.
Solution:
◼ Remarks:
1. Use identity 10.
♦ List of trigonometric identities can be seen here.
6. Solve the quadratic equation for x.
◼ We obtained two values for x.
• Consider the situation where, x = -1.
• The L.H.S of the given equation will become:
tan-1(-1) + tan-1(-2)
• Both terms will give -ve angles.So the L.H.S will become -ve.
• But the R.H.S is a +ve angle. So x = -1 is not acceptable.
• The only solution for the given equation is: $x\,=\,\frac{1}{6}$.
The link below, gives some more solved examples:
We have completed a discussion on inverse trigonometric functions. In the next chapter, we will see matrices.
Copyright©2024 Higher secondary mathematics.blogspot.com
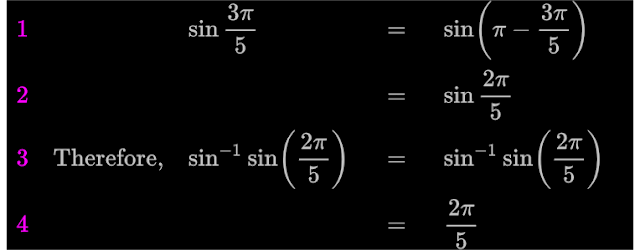






No comments:
Post a Comment