In the previous section, we saw the derivatives of polynomial functions. In this section, we will see the derivatives of trigonometric functions.
• We have already seen the derivative of sin x.
♦ That is., when f(x) = sin x, f'(x) will be cos x
• We obtained this result using first principle.
♦ That is., we used the formula:
$f'(x) = \lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}$
[See fig.13.33 in section 13.13]
• To find derivatives of various trigonometric functions, we need to know the derivative of cos x also.
• To find the derivative of cos x, we must use the first principle.
• Once we know the derivative of both sin x and cos x, we can use sum rule, product rule, quotient rule etc.,
• The derivative of cos x can be obtained as follows:
$\begin{array}{ll} {}&{f'(x)} & {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}} &{} \\
{}&{} & {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[\cos (x+h)] – [cos x]}{h} \right]}} &{} \\
{}&{} & {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{[\cos x \cos h ~-~\sin x \sin h] – [cos x]}{h} \right]}} &{} \\
{}&{} & {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\cos x (\cos h - 1)~-~ \sin x \sin h}{h} \right]}} &{} \\
{}&{} & {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\cos x (\cos h - 1)}{h}
\right]}~-~\lim_{h\rightarrow 0}{\left[\frac{\sin x \sin h}{h} \right]}} &{} \\
{}&{} & {~=~}& {\cos x \lim_{h\rightarrow 0}{\left[\frac{\cos h - 1}{h}
\right]}~-~\sin x \lim_{h\rightarrow 0}{\left[\frac{\sin h}{h} \right]}} &{} \\
{}&{} & {~=~}& {\cos x × 0~-~\sin x × 1} &{} \\
{}&{} & {~=~}& {- \sin x} &{} \\
\end{array}$
• Now we have two useful results:
♦ If f(x) = sin x, then f'(x) = cos x
♦ If f(x) = cos x, then f'(x) = -sin x
• We have already seen the graph of sin x and it's derivative. Now we will see the graph of cos x and it's derivative. It can be written in 5 steps:
1. We know that, f’(x) is a function. So we must be able to plot f’(x).
2. In fig.13.39 below, both f(x) and f’(x) are plotted in the same graph.
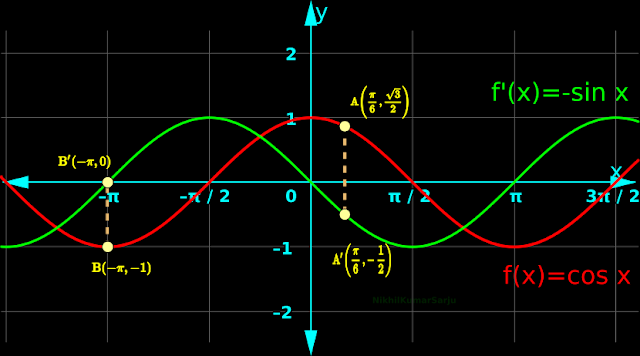 |
| Fig.13.39 |
3. The two graphs are plotted in different colors.
♦ The red curve represents f(x)
♦ The green curve represents f’(x)
4. Let us see the practical application of the graph. It can be written using two examples:
(i) Suppose that, we want the derivative of f(x) at $\left(x=\frac{\pi}{6}\right)$. That is., we want $f' \left(\frac{\pi}{6}\right)$
• For that, we mark point A on the red curve. Here, $\left(x=\frac{\pi}{6}\right)$
• Next we draw a vertical line through A. This vertical line meets the green curve at A'.
• $f' \left(\frac{\pi}{6}\right)$ will be equal to the y-coordinate of A'. In this case, it is $-\frac{1}{2}$
•
We can verify this theoretically:
$f' \left(\frac{\pi}{6}\right)~=~- \sin \left(\frac{\pi}{6}\right)~=~- \frac{1}{2}$
(ii) Suppose that, we want the derivative of f(x) at
$\left(x = -\pi \right)$. That is., we want $f'
\left(-\pi \right)$
• For that, we mark point B on the red curve. Here, $\left(x = -\pi \right)$
• Next we draw a vertical line through B. This vertical line meets the green curve at B'.
• $f'
\left(-\pi \right)$ will be equal to the y-coordinate of B'. In this case, it is 0.
•
We can verify this theoretically:
$f' \left(-\pi \right)~=~- \sin \left(-\pi \right)~=~0$
5. Further more, the reader may verify the tangents also:
•
Through the point A, draw a line at a slope of $- \frac{1}{2}$. This line will be tangential to f(x).
•
Through the point B, draw a line at a slope of 0 (a horizontal line). This line will be tangential to f(x).
Let us see some solved examples:
Solved example 13.17
Compute the derivative of tan x
Solution:
1. We can apply the quotient rule:
$\left(\frac{u}{v} \right)' = \frac{u'v - uv' }{v^2}$
2. In our present case:
u = sin x. So u' = cos x
v = cos x. So v' = -sin x
3. Thus we get:
$\begin{array}{ll}
{}&{\left(\frac{\sin x}{\cos x} \right)'}
& {~=~}& {\left(\frac{u}{v} \right)'}
&{} \\
{}&{}
& {~=~}& {\frac{[\cos x × \cos x] - [\sin x × -\sin x] }{\cos^2 x}}
&{} \\
{}&{}
& {~=~}& {\frac{\cos^2 x + \sin^2 x}{\cos^2 x}}
&{} \\
{}&{}
& {~=~}& {\frac{1}{\cos^2 x}}
&{} \\
{}&{}
& {~=~}& {\sec^2 x}
&{} \\
\end{array}$
Alternate method:
We can use first principle:
$\begin{array}{ll}
{}&{f'(x)}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{f(x+h) – f(x)}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\tan(x+h) – \tan x}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{ \frac{\sin (x+h)}{\cos (x+h)} - \frac{\sin x}{\cos x}}{h} \right]}}
&{} \\
{}&{}
&
{~=~}& {\lim_{h\rightarrow 0}{\left[\frac{ \frac{\sin (x+h) \cos
x~-~\cos (x+h) \sin x}{\cos (x+h) \cos x}}{h} \right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin (x+h) \cos x~-~\cos (x+h) \sin x}{h\;\cos (x+h) \cos x}
\right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin (x+h - x)}{h\;\cos (x+h) \cos x}
\right]}~\color{green}{\text{- - - (I)}}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin h}{h\;\cos (x+h) \cos x}
\right]}}
&{} \\
{}&{}
& {~=~}& {\lim_{h\rightarrow 0}{\left[\frac{\sin h}{h}
\right]}~ × ~\lim_{h\rightarrow 0}{\left[\frac{1}{\cos (x+h) \cos x}
\right]}}
&{} \\
{}&{}
& {~=~}& {1~ × ~\frac{1}{\cos^2 x}}
&{} \\
{}&{}
& {~=~}& {\sec^2 x}
&{} \\
\end{array}$
◼ Remarks:
• Line marked as I:
Here we use the identity:
sin (A-B) = sin A cos B - cos A sin B
A graphical description can be written in 5 steps:
1. We know that, f’(x) is a function. So we must be able to plot f’(x).
2. In fig.13.40 below, both f(x) and f’(x) are plotted in the same graph.
 |
| Fig.13.40 |
3. The two graphs are plotted in different colors.
♦ The red curve represents f(x)
♦ The green curve represents f’(x)
4. Let us see the practical application of the graph. It can be written using two examples:
(i)
Suppose that, we want the derivative of f(x) at
$\left(x=\frac{\pi}{3}\right)$. That is., we want $f'
\left(\frac{\pi}{3}\right)$
• For that, we mark point A on the red curve. Here, $\left(x=\frac{\pi}{3}\right)$
• Next we draw a vertical line through A. This vertical line meets the green curve at A'.
• $f' \left(\frac{\pi}{3}\right)$ will be equal to the y-coordinate of A'. In this case, it is 4
•
We can verify this theoretically:
$f' \left(\frac{\pi}{3}\right)~=~ \sec^2 \left(\frac{\pi}{3}\right)~=~\frac{1}{\cos^2 \left(\frac{\pi}{3}\right)}~=~\frac{1}{(1/2)^2}~=~4$
(ii) Suppose that, we want the derivative of f(x) at
$\left(x = -\pi \right)$. That is., we want $f'
\left(-\pi \right)$
• For that, we mark point B on the red curve. Here, $\left(x = -\pi \right)$
• Next we draw a vertical line through B. This vertical line meets the green curve at B'.
• $f'
\left(-\pi \right)$ will be equal to the y-coordinate of B'. In this case, it is 1.
•
We can verify this theoretically:
$f' \left(-\pi\right)~=~ \sec^2 \left(-\pi\right)~=~\frac{1}{\cos^2 \left(-\pi\right)}~=~\frac{1}{(-1)^2}~=~1$
5. Further more, the reader may verify the tangents also:
•
Through the point A, draw a line at a slope of 4. This line will be tangential to f(x).
•
Through the point B, draw a line at a slope of 1. This line will be tangential to f(x).
Solved example 13.18
Compute the derivative of f(x) = sin2 x
Solution:
1. We can write sin2 x as sin x . sin x
Now we can apply the product rule: (uv)' = u'v + uv'
2. The steps are shown below:
$\begin{array}{ll}
{}&{\left(\sin^2 x \right)'}
& {~=~}& {\left(\sin x \, . \, \sin x \right)'}
&{} \\
{}&{}
& {~=~}& {(\sin x)' × \sin x~+~\sin x × (\sin x)'}
&{} \\
{}&{}
& {~=~}& {\cos x × \sin x~+~\sin x × \cos x}
&{} \\
{}&{}
& {~=~}& {2 \sin x \cos x}
&{} \\
{}&{}
& {~=~}& {\sin 2x}
&{} \\
\end{array}$
A graphical description can be written in 5 steps:
1. We know that, f’(x) is a function. So we must be able to plot f’(x).
2. In fig.13.41 below, both f(x) and f’(x) are plotted in the same graph.
 |
| Fig.13.41 |
3. The two graphs are plotted in different colors.
♦ The red curve represents f(x)
♦ The green curve represents f’(x)
4. Let us see the practical application of the graph. It can be written using two examples:
(i)
Suppose that, we want the derivative of f(x) at
$\left(x=\frac{\pi}{6}\right)$. That is., we want $f'
\left(\frac{\pi}{6}\right)$
• For that, we mark point A on the red curve. Here, $\left(x=\frac{\pi}{6}\right)$
• Next we draw a vertical line through A. This vertical line meets the green curve at A'.
• $f' \left(\frac{\pi}{6}\right)$ will be equal to the y-coordinate of A'. In this case, it is 4
•
We can verify this theoretically:
$f' \left(\frac{\pi}{6}\right)~=~
\sin \left(\frac{2 \pi}{6}\right)~=~
\sin \left(\frac{\pi}{3}\right) ~=~\frac{\sqrt3}{2}$
(ii)
Suppose that, we want the derivative of f(x) at
$\left(x=-\frac{\pi}{4}\right)$. That is., we want $f'
\left(-\frac{\pi}{4}\right)$
• For that, we mark point B on the red curve. Here, $\left(x=-\frac{\pi}{4}\right)$
• Next we draw a vertical line through B. This vertical line meets the green curve at B'.
• $f' \left(-\frac{\pi}{4}\right)$ will be equal to the y-coordinate of B'. In this case, it is 4
•
We can verify this theoretically:
$f' \left(-\frac{\pi}{4}\right)~=~
\sin \left(\frac{-2 \pi}{4}\right)~=~
\sin \left(-\frac{\pi}{2}\right)~=~
-\sin \left(\frac{\pi}{2}\right) ~=~-1$
5. Further more, the reader may verify the tangents also:
•
Through the point A, draw a line at a slope of $\frac{\sqrt3}{2}$. This line will be tangential to f(x).
•
Through the point B, draw a line at a slope of -1. This line will be tangential to f(x).
•
We have drawn a large number of graphs. Those graphs were drawn to demonstrate the close relation between f(x) and f'(x).
•
From now on wards, we will not draw any more graphs. We will concentrate only on the method for obtaining f'(x).
•
However, the interested reader may continue to draw them.
Link to a few more solved examples is given below:
In the next section, we will see some miscellaneous examples.
No comments:
Post a Comment