In the previous section, we completed a discussion on linear inequalities. In this chapter we will see permutations and combinations.
We can obtain a basic understanding about permutations and combinations by considering an example. It can be written in 4 steps:
1. Suppose that, we have a number lock.
• Let it have four wheels.
• Let each wheel have seven digits from 0 to 6
(Some images can be seen here)
2. We will be able to open the lock only if we can remember a secret combination of four digits.
• We must bring those four digits in a particular line.
• Also, those four digits must be arranged in the correct sequence.
For example, if the secret combination is 4, 2, 3, 6:
‘4’ must always be in the first position.
‘2’ must always be in the second position.
‘3’ must always be in the third position.
‘6’ must always be in the fourth position.
Interchanging of positions is not allowed.
• So it is important to remember all the four digits. It is also important to remember the correct positions.
3. Suppose that, we have forgotten the digits and the positions. Then the only way to open the lock is to try various combinations. Let us analyze such a situation:
• We remember the first digit. Let it be ‘4’
• Also we remember that, no digit repeats.
• Then some of the possible combinations are:
4, 6, 3, 1
4, 3, 5, 2
4, 1, 6, 3
4, 2, 5, 6
so on . . .
4. Obviously, it is a tedious process to obtain the correct combination by doing such trials. We will have to make a very large number of trials.
• Two questions will arise in our minds:
♦ How many trial combinations are possible?
♦ Is there a systematic way to carry out the trials?
• The principles of permutations and combinations help us to answer those questions.
• First we will learn about the Fundamental principle of counting
• This principle can be explained using two examples.
Example 1:
This can be written in 3 steps:
1. A student has two pairs of pants. One is blue and the other is brown.
• Also he has three shirts. Green, yellow and red.
◼ In how many different ways can he dress up?
2. This problem can be analyzed effectively with the help of fig.7.1 below.
It can be written in three steps.
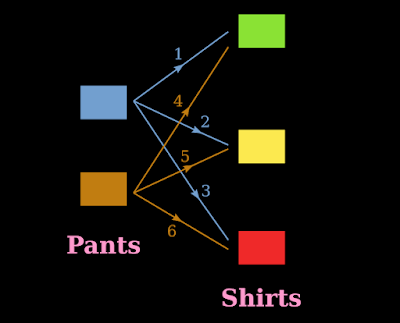 |
| Fig.7.1 |
(i) Suppose that the student selects blue pants.
• Taking that blue pants, he can move along the arrow no. 1 to select the green shirt.
• Taking that blue pants, he can move along the arrow no. 2 to select the yellow shirt.
• Taking that blue pants, he can move along the arrow no. 3 to select the red shirt.
• So it is clear that, if the blue pants is selected, there are three different ways in which he can dress up.
(ii) Suppose that the student selects brown pants.
• Taking that brown pants, he can move along the arrow no. 4 to select the green shirt.
• Taking that brown pants, he can move along the arrow no. 5 to select the yellow shirt.
• Taking that brown pants, he can move along the arrow no. 6 to select the red shirt.
• So it is clear that, if the brown pants is selected, there are three different ways in which he can dress up.
(iii) Thus altogether, there are six different ways in which he can dress up.
3. We obtained an important result:
The total number of possible combinations is 6
• This result can be obtained with out writing all the above detailed steps. There is an easy method. It can be written in three steps:
(i) The first event is: Selecting a pair of pants.
• This event can occur in two different ways.
(ii) The second event is: Selecting a shirt.
• For each of the two ways for the first event, the second event can occur in three different ways.
(iii) So the total number of combinations possible is (2 × 3) = 6
Example 2:
This can be written in 3 steps:
1. A student has two pairs of pants. One is blue and the other is brown.
• Also he has three shirts. Green, yellow and red.
• Also he has two bags. Orange and magenta.
◼ In how many different ways can he dress up?
2. This problem can be analyzed effectively with the help of fig.7.2 below.
It can be written in three steps.
 |
| Fig.7.2 |
(i) Consider the dashed line in fig.7.2.
• The left side of the dashed line is the same fig. that we saw in example 1
• That means, the dashed line indicates the six possible combinations of the two pants and three shirts.
(ii) After dressing up in any one of those six combinations, the student can select either the orange bag or the magenta bag.
• That means, for each of the final six combinations that we saw in the previous example 1, there are two bags.
(iii) Thus altogether, there will be twelve different ways in which he can dress up.
3. We obtained an important result:
The total number of possible combinations is 12
• This result can be obtained with out writing all the above detailed steps. There is an easy method. It can be written in three steps:
(i) The first event is: Selecting a pair of pants.
• This event can occur in two different ways.
(ii) The second event is: Selecting a shirt.
• For each of the two ways for the first event, the second event can occur in three different ways.
(iii) So the total number of combinations possible from the first and second events is (2 × 3)
(iv) The third event is: Selecting a bag.
• For each of the (2 × 3) combinations of the first and second events, the third event can occur in two different ways.
(iii) So the total number of combinations possible from the first, second and third events is (2 × 3) × 2 = (2 × 3 × 2) = 12
Based on the above two examples, we can write the fundamental principle of counting:
A. When there are two events.
This can be written in 3 steps:
(i) The first event can occur in m different ways.
(ii) For each of the m ways, the second event can occur in n different ways.
(iii) Then the total number of combinations possible is (m × n)
B. For three events:
This can be written in steps:
(i) The first event can occur in m different ways.
(ii) For each of the m ways, the second event can occur in n different ways.
(iii)Then the total number of combinations possible from the first and second events is (m × n)
(iv) For each of the (m × n) ways, the third event can occur in p different ways.
(v) Then the total number of combinations possible from the three events is (m × n × p)
◼ In this way, the principle can be written for any number of finite events.
◼ The fundamental principle of counting is also known as multiplication principle.
Let us see a solved example:
Solved example 7.1
Find the number of 4 letter words, with or without meaning, which can be
formed out of the letters of the word ROSE, where the repetition of the letters is not allowed.
Solution:
1. Consider a four letter word.
• The first letter of that word can be R, O, S or E
• The first event is ‘selecting the first letter’.
• It is clear that, the first event can occur in four different ways.
2. The second event is ‘selecting the second letter’.
• Remember that no repetition is allowed. So we can write:
♦ If R is selected in the first event, the letter for the second event can be only O, S or E
♦ If O is selected in the first event, the letter for the second event can be only R, S or E
♦ If S is selected in the first event, the letter for the second event can be only R, O or E
♦ If E is selected in the first event, the letter for the second event can be only R, O or S
• It is clear that, for each letter selected in the first event, the second event can occur in three different ways.
3. The third event is ‘selecting the third letter’.
• Remember that no repetition is allowed. So it is clear that, the third event can occur in two different ways.
4. The fourth event is ‘selecting the fourth letter’.
• Remember that no repetition is allowed. So it is clear that, the fourth event can occur in one way only.
5. So by applying multiplication principle, we get:
Total number of combinations possible = (4 × 3 × 2 × 1) = 24
• In the above problem, what will happen if repetition is allowed?
The answer can be written in two steps:
1. If repetition is allowed,
♦ The first event can occur in four different ways.
♦ The second event can occur in four different ways.
♦ The third event can occur in four different ways.
♦ The fourth event can occur in four different ways.
2. So the total number of combinations possible = (4 × 4 × 4 × 4) = 256
Solved example 7.2
We are given 4 flags of different colors. How many different signals can be generated, if a signal requires the use of 2 flags. One placed above and the other below?
Solution:
1. Fig.7.3(a) shows a combination of two flags. One placed above and the other below.
• Fig.(b) shows another combination. We have to find out the maximum possible number of such combinations.
2. To do the trials, we can take two boxes as shown in fig.c.
• We have to fill the boxes with the given four flags, taking two at a time.
3. First we will fill the top box.
• So filling of the top box is the first event. It can take place in four different ways.
4. Next we fill the bottom box. So filling the bottom box is the second event.
• After filling the top box, we will be having three flags. So the second event can take place in three different ways.
5. So by applying multiplication principle, we get:
Total number of combinations possible = (4 × 3) = 12
• In the next section, we will see a few more solved examples.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment