In the previous section, we completed a discussion on factorial notation. In this section, we will see how the factorial notation can help us to shorten the expression for nPr.
The shortened expression can be obtained in 7 steps:
1. Consider the expression that we derived:
nPr = n(n-1)(n-2)(n-3) . . . (n-r+1)
• Consider the RHS.
♦ n is continuously decreasing. It becomes (n-1), (n-2), (n-3), . . .
♦ But it does not become 1.
2. Let us write the remaining terms so that, it becomes 1
♦ The last term at present is (n-r+1)
♦ So the next term will be (n-r+1-1) = (n-r)
♦ The term after (n-r) will be (n-r-1)
♦ In this way, we can reach up to 1
3. So the present RHS must be multiplied by [(n-r)(n-r-1) . . . 3 × 2 × 1]
• But we must multiply the denominator also by the same quantity. Otherwise, the value will change.
• So we can write:
${}^nP_r=\frac{n(n-1)(n-2)(n-3)~.~.~.~ (n-r+1)[(n-r)(n-r-1)~.~.~.~ 3 × 2 × 1]}{[(n-r)(n-r-1)~.~.~. 3 × 2 × 1]}$
4. The numerator in the RHS of the expression in (3) is:
$n(n-1)(n-2)(n-3)~.~.~. (n-r+1)(n-r)(n-r-1)~.~.~. 3 × 2 × 1$
• This is n!
5. The denominator in the RHS of the expression in (3) is: $(n-r)(n-r-1)~.~.~. 3 × 2 × 1$
• This is (n-r)!
6. So the expression in (3) becomes: ${}^nP_r=\frac{n!}{(n-r)!}$
7. Now we can write it as the first formula related to permutations.
A. Formula for the number of permutations of n objects taken r at a time is:
${}^nP_r=\frac{n!}{(n-r)!}$
◼ Here two points are to be noted
First point can be written in 4 steps:
(i) n is a number of objects. So it has to be greater than 0
♦ That is., 0 < n
(ii) r is a number of objects. So it has to be greater than 0
♦ That is., 0 < r
(iii) We are taking r objects out of n objects. So r must be less than or equal to n
♦ That is., r ≤ n
(iv) Combining the three inequalities, we get: 0 < r ≤ n
Second point can be written in 3 steps:
(i) The n objects must be different
(ii) For example, suppose that the objects are the letters of the word NUMBER.
Here n is 6. All 6 objects are different.
(iii) Suppose that the objects are the letters of the word ROOT
Here n is 4. All 4 objects are not different because, the letter ‘O’ appears two times.
Let us see an interesting result based on the above formula. It can be written in 4 steps:
1. We already know this:
If instead of r objects, we take all the n objects, the number of permutations will be:
n(n-1)(n-2)(n-3) . . . 3 × 2 × 1
2. But n(n-1)(n-2)(n-3) . . . 3 × 2 × 1 is n!
• That means, if we take all the n objects, the number of permutations is n!
3. Let us see whether we will get the same result using the formula.
• We have: ${}^nP_r=\frac{n!}{(n-r)!}$
• When r = n, we get:
${}^nP_r={}^nP_n=\frac{n!}{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n!$
• This is the same result that we wrote in (2)
4. So the formula is applicable for r = n also. We can write it as the second formula.
B. Formula for the number of permutations of n objects taken all at a time is: n!
Let us see another interesting result based on the above formula. It can be written in 4 steps:
1. We usually take r objects from among the given n objects.
• Some times we take all the n objects.
2. But what if we take none of the objects?
• How many permutations are possible if we take none of the given objects?
The answer can be written in 3 steps:
(i) Number of boxes to be taken:
♦ Recall that, for r objects, we take r boxes.
♦ For n objects, we take n boxes.
♦ So for zero objects, we take zero boxes
So visualize that, there are no boxes to put in the objects.
(ii) There is only one arrangement possible in which no boxes are present.
(iii) That means, if we take zero objects from among the given n objects, the number of permutations possible is 1
3. Let us see whether we will get the same result using the formula.
• We have: ${}^nP_r=\frac{n!}{(n-r)!}$
• When r = 0, we get:
${}^nP_r={}^nP_0=\frac{n!}{(n-0)!}=\frac{n!}{n!}=1$
• This is the same result that we wrote in (2)
4. So the formula is applicable for r = 0 also.
Now we will derive the third formula.
C. Number of permutations of n objects taken r at a time, when repetition is allowed is: nr
Proof can be written in 2 steps:
1.If r objects are taken, there will be r boxes
• The first box can be filled in n different ways.
• Since repetition is allowed, the second box can also be filled in n different ways.
• Since repetition is allowed, the third box can also be filled in n different ways.
- - -
- - -
• so on . . .
• This can be visualized as shown in fig.7.6 below:
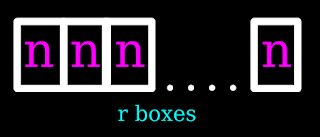 |
| Fig.7.6 |
2. So by applying the multiplication principle, the number of permutations possible = (n × n × n . . . n × n) = nr
• Note that, if all the n objects are taken, we will get nn
Before we move on to the next formula, let us apply the above formulas to the examples that we saw in earlier sections
Example 1:
We want to find the number of permutations when the letters of the word ROSE are taken all at a time. Repetition not allowed.
Solution:
1. We must use formula B because all objects are taken at a time.
So we get: Number of permutations = n! = 4! = 4 × 3 × 2 × 1=24
2. When repetition is allowed, we apply formula C: nr
• So we get: $n^r = 4^4 = 256$
Example 2:
We want to find the number of permutations when the letters of the word NUMBER are taken 3 at a time. Repetition not allowed.
Solution:
1. We have formula A: ${}^nP_r=\frac{n!}{(n-r)!}$
♦ Here n = 6 and r = 3
• So we get:
${}^nP_r={}^6P_3=\frac{6!}{(6-3)!}=\frac{6!}{3!}=\frac{6 × 5 × 4 × 3!}{3!}=6 × 5 × 4=120$
2. When repetition is allowed, we apply formula C: nr
• So we get: $n^r = 6^3 = 216$
Another example:
In a group, there are 12 members. A Chairman and a Vice-Chairman are to be selected from among them. In how many different ways can this be done. None of the members can hold more than one position.
Solution:
We have formula A: ${}^nP_r=\frac{n!}{(n-r)!}$
♦ Here n = 12 and r = 2
• So we get:
${}^nP_r={}^{12}P_2=\frac{12!}{(12-2)!}=\frac{12!}{10!}=\frac{12 × 11 × 10!}{10!}=12 × 11=132$
The next formula that we are going to derive is applicable when some of the objects are not different. Some basics can be written in steps:
1. The formulas that we obtained so far were related to those cases, where all objects are different.
• For example,
♦ All letters of the word ROSE are different.
♦ All letters of the word NUMBER are different.
2. Now consider the word ROOT. We want to calculate the number of permutations of the letters in this word.
• In this word, there are 4 objects. But two of them (the two Os) are the same.
3. For convenience, let us assume that the two identical objects are different.
• So we will name one of the Os as O1 and the other as O2. Now there are 4 different objects.
4. We want the number of permutations of those 4 objects, taking all at a time. Repetition is not allowed.
• We can use formula B: n!
♦ Here n = 4
• So we get:
Number of permutations = n! = 4! = 4 × 3 × 2 × 1 = 24
5. We can write:
If we make a list of all permutations, there will be 24 permutations in that list.
• Some of those permutations are:
♦ RO1O2T
♦ RO2O1T
♦ O1TO2R
♦ O2TO1R, etc.,
6. Now consider the set of two permutations: RO1O2T and RO2O1T
• The O1 and O2 are same as O
• That means, the two permutations RO1O2T and RO2O1T will reduce to one permutation: ROOT.
7. Let us see another set of two permutations: O1TO2R and O2TO1R
• The O1 and O2 are same as O
• That means, the two permutations O1TO2R and O2TO1R reduce to OTOR.
8. In this way, if we discard the subscripts ‘1’ and ‘2’,
♦ for every permutation, there will be an identical permutation.
• We can write:
[No. of actual permutations] × 2 = 24
• So [No. of actual permutations] = $\frac{24}{2}$ = 12
9. In the above step,
♦ [No. of actual permutations] is multiplied by ‘2’.
• The ‘2’ is actually 2!
♦ This is because, the two Os can be arranged among themselves in 2! ways.
10. Thus we can write:
Number of permutations when all letters of the word ROOT are taken is: 12
Let us see another example. It can be written in steps:
1. Consider the word INSTITUTE
• There are 9 letters.
♦ I is present 2 times
♦ T is present 3 times
♦ All remaining letters are different.
• So the number of permutations when all letters of the word INSTITUTE are taken is: $\frac{9!}{2!\;3!}$
Based on the above examples of ROOT and INSTITUTE, we can write the fourth formula.
D. Number of permutations of n objects when p objects among them are of the same kind and the rest are all different is: $\frac{n!}{p!}$
• This formula is applicable when there is only one type of recurring object. That recurring object will be present p times.
• Some times there will be more than one type of recurring objects.
♦ The first type will be present p1 times.
♦ The second type will be present p2 times.
♦ The third type will be present p3q times.
♦ - - -
♦ - - -
♦ The kth type will be present pk times.
• In such cases, we can use the fifth formula:
E. Number of permutations of n objects when there are more than one type of recurring objects is: $\frac{n!}{{p_1}!\, {p_2}!\, {p_3}! ~.~.~.~{p_k}!}$
Now we will see a solved example:
Solved example 7.10
Find the number of permutations of the letters of the word ALLAHABAD.
Solution:
• There are 9 letters.
♦ A is present 4 times
♦ L is present 2 times
♦ All remaining letters are different.
• So the number of permutations =
$\frac{9!}{4!\;2!}=~\frac{9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1}{4 × 3 × 2 × 1 × 2 × 1}=\frac{9 × 8 × 7 × 6 × 5}{2 × 1}=9 × 8 × 7 × 3 × 5 = 7560$
In the next section, we will see a few more solved examples.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment