In the previous section, we completed a discussion on second order differentiation. In this section, we will see Rolle's theorem and mean value theorem.
The basic details about Rolle's theorem can be written in 4 steps:
1. In the fig.21.23 below, the red curve is the graph of a function f.
 |
| Fig.21.23 |
2. The function f satisfies the following four conditions:
(i) f is a real valued function.
(ii) f is continuous in the interval [a,b]
(iii) f is differentiable in the interval (a,b)
(iv) f(a) = f(b)
•
Note that, the solid green line which passes through both (a, f(a)) and (b, f(b)) is horizontal.
•
Since the solid green line is horizontal, f(a) = f(b)
3. If the four conditions are satisfied, we can write:
There is atleast one point c in the interval (a,b), such that f'(c) = 0
•
Note that, a tangent (yellow line) is drawn to the red curve at (c, f(c)). This tangent is horizontal. Since this tangent is horizontal, we can say that, slope of the tangent at c is zero. In other words, derivative at c is zero.
4. Another example is shown in fig.21.24 below:
 |
| Fig.21.24 |
•
We see that:
(i) g is a real valued function.
(ii) g is continuous in the interval [a,b]
(iii) g is differentiable in the interval (a,b)
(iv) g(a) = g(b)
•
In this case, there are two points c and d, where the derivative is zero.
Solved example 21.64
Verify Rolle's theorem for the function f(x) = x2 + 2
when a = −2 and b = 2
Solution:
1. Let us check whether the four conditions are satisfied:
(i) Given f is a real valued function.
(ii) f is continuous in the interval [−2, 2]
(iii) f is differentiable in the interval (−2, 2)
(iv) f(−2) = (−2)2 + 2 = 6 = f(2) = (2)2 + 2
•
So the four conditions are satisfied.
2. Since the four conditions are satisfied, Rolle's theorem is applicable.
•
That means, there exists atleast one number c, in the interval (−2, 2) such that, f'(c) = 0. Our aim is to find this c.
3. We have: f'(x) = 2x
•
Equating f'(x) to zero, we get: 2x = 0
⇒ x = 0
4. That means, f'(0) = 0.
Therefore, c = 0
•
c = 0 indeed lies in the interval (−2, 2)
5. The graph is shown in fig.21.25 below:
 |
| Fig.21.25 |
•
The tangent at c = 0 is drawn in yellow color.
•
This tangent is horizontal, which means, slope of the tangent is zero. In other words, the derivative at c = 0, is zero.
Now we will see mean value theorem (M.V.T). The basic details can be written in 5 steps:
1. In the fig.21.26 below, the red curve is the graph of a function f.
 |
| Fig.21.26 |
2. The function f satisfies the following three conditions:
(i) f is a real valued function.
(ii) f is continuous in the interval [a,b]
(iii) f is differentiable in the interval (a,b)
3. If the three conditions are satisfied, we can write:
There is atleast one point c in the interval (a,b), such that:
$\rm{f'(c)~=~\frac{f(b) - f(a)}{b-a}}$
4. Let us see the significance of the quantity $\rm{\frac{f(b) - f(a)}{b-a}}$.
It can be written in 5 steps:
(i) The vertical distance between (a, f(a)) and (b, f(b)) is [f(b) − f(a)]
(ii) The horizontal distance between (a, f(a)) and (b, f(b)) is [b−a]
(iii) So $\rm{\frac{f(b) - f(a)}{b-a}}$ is the slope of the line joining (a, f(a)) and (b, f(b))
(iv) But the line joining (a, f(a)) and (b, f(b)), is the secant between (a, f(a)) and (b, f(b)).
(v) So we can write:
$\rm{f'(c)~=~\frac{f(b) - f(a)}{b-a}}$ is the slope of the secant between (a, f(a)) and (b, f(b)).
5. So based on (3), we can write:
If the three conditions are satisfied,
There is atleast one point c in the interval (a,b), such that:
the derivative at c is same as the slope of the secant between (a, f(a)) and (b, f(b)).
Solved example 21.65
Verify Mean Value Theorem for the function f(x) = x2
when a = 2 and b = 4
Solution:
1. Let us check whether the three conditions are satisfied:
(i) Given f is a real valued function.
(ii) f is continuous in the interval [2, 4]
(iii) f is differentiable in the interval (2, 4)
•
So the three conditions are satisfied.
2. Since the three conditions are satisfied, M.V.T is applicable.
•
That means, there exists atleast one number c, in the interval (2, 4) such that, $\rm{f'(c)~=~\frac{f(4) - f(2)}{4-2}}$. Our aim is to find this c.
3. The R.H.S can be calculated as shown below:
$\rm{\frac{f(4) - f(2)}{4-2}~=~\frac{4^2 - 2^2}{4-2}~=~\frac{16 - 4}{4-2}~=~\frac{12}{2}~=~6}$
4. We have: f'(x) = 2x
•
Equating f'(x) to 6, we get: 2x = 6
⇒ x = 3
5. That means, f'(3) = 6.
Therefore, c = 3
•
c = 3 indeed lies in the interval (2, 4)
6. The graph (red curve) is shown in fig.21.27 below:
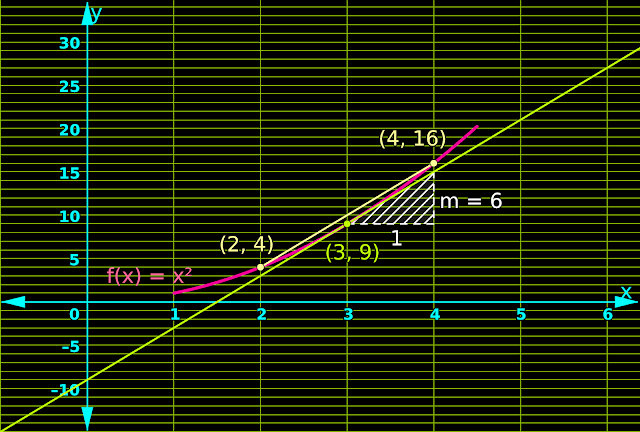 |
| Fig.21.27 |
•
The scale of x and y axes are adjusted so as to make the curvature of the graph visible.
•
The secant (yellow line) is drawn between a = 2 and b = 4
•
The tangent (green line) is drawn at c = 3
•
The tangent is parallel to the secant. Both have the slope 6.
The link below gives a few more solved examples:
In the next section, we will see some miscellaneous examples.
Previous
Contents
Next
Copyright©2024 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment