In the previous section, we saw how to calculate the Probability of an event. In this section, we will see probability of the event "A or B".
Probability of the event “A or B”
• Suppose that, we have two events: Event A and Event B. We have seen that, a new event (A∪B) can be created.♦ If any outcome in A occurs, we say that A∪B has also occurred.
♦ If any outcome in B occurs, then also we say that A∪B has also occurred.
• So A∪B indicates “A or B”.
• If we know P(A) and P(B), can we find P(A∪B)?
We have already seen axiom 3 which says:
P(A∪B) = P(A) + P(B)
• But this axiom is valid only if A and B are disjoint sets (mutually exclusive events).
• When A and B are not disjoint sets, we need a method to calculate P(A∪B).
Let us see an example. It can be written in 9 steps:
1. Consider the experiment of tossing a coin thrice.
2. We know that, S = {(H,H,H), (H,H,T), (H,T,H), (H,T,T), (T,H,H), (T,H,T), (T,T,H), (T,T,T)}
•
We see that, there are eight possible outcomes.
3. Next step is to assign probabilities for each of these outcomes.
•
Let the probabilities be as shown below:
$\begin{array}{cc}
{\textbf{Outcomes}}&{\textbf{HHH}}
&
{\textbf{HHT}}& {\textbf{HTH}} & {\textbf{HTT}} &
{\textbf{THH}} & {\textbf{THT}} & {\textbf{TTH}} &
{\textbf{TTT}}\\
{\textbf{Probabilities}}&{\frac{1}{8}}
&{\frac{1}{8}} &{\frac{1}{8}} &{\frac{1}{8}}
&{\frac{1}{8}} &{\frac{1}{8}} &{\frac{1}{8}}
&{\frac{1}{8}}\\
\end{array}$
•
Note that, we put 8 in the denominator because, the total number of outcomes is 8.
•
The reader may verify that, the above assigned probabilities satisfy
both condition 1 and condition 2. that we saw in the previous section.
(The
reader must keep in mind that, 1/8 is only a theoretical value. In
actual practice, we will get “values close to 1/8” only when the
experiment is repeated a very large number of times)
4. Suppose that an event A is such that:
A = {HHT, HTH, THH}
•
Now we use result 4:
$\rm{P(A)~=~\sum{P \left(\lbrace \omega_i \rbrace \right)}}$
•
So in our present case, we get:
$\begin{array}{ll}
{}&{\rm{P(A)}}
&
{~=~}& {\rm{P \left(\lbrace HHT \rbrace \right) + P \left(\lbrace
HTH \rbrace \right) + P \left(\lbrace THH \rbrace \right)}} &{} \\
{}&{}
& {~=~}& {\frac{1}{8}~+~\frac{1}{8}~+~\frac{1}{8}} &{} \\
{}&{}
& {~=~}& {\frac{3}{8}} &{} \\
\end{array}$
5. Suppose that an event B is such that:
B = {HTH, THH, HHH}
•
Now we use result 4 again:
$\rm{P(B)~=~\sum{P \left(\lbrace \omega_i \rbrace \right)}}$
•
So in our present case, we get:
$\begin{array}{ll}
{}&{\rm{P(B)}}
&
{~=~}& {\rm{P \left(\lbrace HTH \rbrace \right) + P \left(\lbrace
THH \rbrace \right) + P \left(\lbrace HHH \rbrace \right)}} &{} \\
{}&{}
& {~=~}& {\frac{1}{8}~+~\frac{1}{8}~+~\frac{1}{8}} &{} \\
{}&{}
& {~=~}& {\frac{3}{8}} &{} \\
\end{array}$
6. Also we have:
A∪B = {HHT, HTH, THH} ∪ {HTH, THH, HHH}
= {HHT, HTH, THH, HHH}
•
Now we use result 4 one more time:
$\rm{P(B)~=~\sum{P \left(\lbrace \omega_i \rbrace \right)}}$
•
So in our present case, we get:
$\begin{array}{ll}
{}&{\rm{P(A \cup B)}}
&
{~=~}& {\rm{P \left(\lbrace HHT \rbrace \right) + P \left(\lbrace
HTH \rbrace \right) + P \left(\lbrace THH \rbrace \right) + P \left(\lbrace HHH \rbrace \right)}} &{} \\
{}&{}
& {~=~}& {\frac{1}{8}~+~\frac{1}{8}~+~\frac{1}{8}~+~\frac{1}{8}} &{} \\
{}&{}
& {~=~}& {\frac{4}{8}} &{} \\
{}&{}
& {~=~}& {\frac{1}{2}} &{} \\
\end{array}$
7. Now we can check whether P(A∪B) is equal to [P(A) + P(B)]
♦ From (6) we have: P(A∪B) = ½
♦ From (4) and (5), we have: P(A) + P(B) = 3/8 + 3/8 = 6/8 = 3/4.
•
We see that, they are not equal.
8. So what happened?
Answer can be written in 4 steps:
(i) In our present case, A and B are not disjoint sets.
•
Two outcomes appear in both A and B. They are: HTH and THH
(ii) So when we calculate [P(A) + P(B)], the probabilities of those two events will be taken twice.
•
But for calculating P(A∪B), we must take the probabilities of each outcome only once.
(iii) So we must make the following deductions from P(A) + P(B):
♦ P({HTH}) must be deducted once.
♦ P({THH}) must be deducted once.
•
That means:
For each element in A∩B, we must deduct it’s probability once.
(iv) Let us write it as a formula:
P(A∪B) = P(A) + P(B) - P(A∩B)
9. Let us check the above formula:
(i) We have: A∩B = {HTH, THH}
(ii) So we get:
$\begin{array}{ll}
{}&{\rm{P(A \cap B)}}
&
{~=~}& {\rm{P \left(\lbrace HTH \rbrace \right) + P \left(\lbrace THH \rbrace \right)}} &{} \\
{}&{}
& {~=~}& {\frac{1}{8}~+~\frac{1}{8}} &{} \\
{}&{}
& {~=~}& {\frac{1}{4}} &{} \\
\end{array}$
(iii) Substituting the values in the formula, we get:
$\begin{array}{ll}
{}&{\rm{P(A \cup B)}}
& {~=~}& {\rm{P(A)~+~P(B)~-~P(A \cap B)}} &{} \\
{}&{}
& {~=~}& {\frac{3}{8}~+~\frac{3}{8}~-~\frac{1}{4}} &{} \\
{}&{}
& {~=~}& {\frac{4}{8}} &{} \\
{}&{}
& {~=~}& {\frac{1}{2}} &{} \\
\end{array}$
• This is the same result that we obtained in (6). So the formula seems to be working. However, we must write the general proof.
The general proof can be written in 4 steps:
1. Consider the Venn diagram shown below:
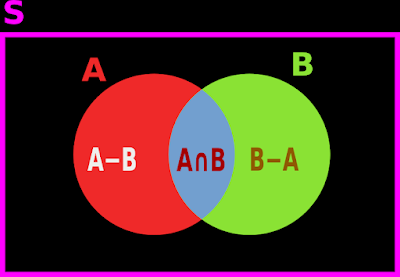 |
| Fig.16.1 |
• We see three sets:
♦ A-B, (Red color)
♦ A∩B (Blue color)
♦ B-A (Green color)
• From the diagram, it is clear that:
The three are disjoint sets.
• From the diagram, it also is clear that:
A∪B = (A-B) ∪ (A∩B) ∪ (B-A)
2. Since the three are disjoint sets, we can apply axiom 3 (see section 16.4). We get:
$\begin{array}{ll}
{}&{\rm{P(A \cup B)}}
& {~=~}& {\rm{P \left[(A-B)~ \cup ~ (A \cap B)~ \cup ~(B-A) \right]}} &{} \\
{}&{}
& {~=~}& {\rm{P \left[(A-B)\right]~ \cup ~ P \left[(A \cap B)\right]~ \cup ~P \left[(B-A) \right]}} &{} \\
{}&{}
& {~=~}& {\rm{\left[\sum{P(\{\omega_i\})}~\forall \omega_i \in (A-B)\right]~+~\left[\sum{P(\{\omega_i\})}~\forall \omega_i \in (A \cap B)\right]~+~\left[\sum{P(\{\omega_i\})}~\forall \omega_i \in (B-A)\right]}~\color{green}{\text{- - - I}}} &{} \\
\end{array}$
◼ Remarks:
•
Line marked as I:
In this line, there are three terms in the RHS. At a first glance, all three terms may appear to be the same. But on close inspection, we will see the differences:
♦ In the first term, we add the probabilities for all elements in (A-B)
(The symbol ‘∀’ stands for ‘for all’)
♦ In the second term, we add the probabilities for all elements in (A∩B)
♦ In the third term, we add the probabilities for all elements in (B-A)
3. In the above step (2), we have derived an important result. We will be using it soon.
•
Now we will add the probabilities of events A and B. We get:
$\begin{array}{ll}
{}&{\rm{P(A)~+~P(B)}}
& {~=~}&
{\rm{\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in A
\Bigr]~+~\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in (B) \Bigr]}}
&{} \\
{}&{}
& {~=~}&
{\rm{\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in [(A-B) \cup (A
\cap B)]\Bigr]~+~\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in [(B-A)
\cup (A \cap B)] \Bigr]}~\color{green}{\text{- - - I}}}
&{} \\
{}&{}
& {~=~}& {\rm{
\Bigl[\sum{P(\{\omega_i\})}~\forall
\omega_i \in (A-B) \Bigr]
~+~\Bigl[\sum{P(\{\omega_i\})}~\forall
\omega_i \in (A \cap
B) \Bigr]
~+~\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in (B-A) \Bigr]
~+~\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in
(A \cap B) \Bigr]}~\color{green}{\text{- - - II}}}
&{} \\
{}&{}
& {~=~}& {\rm{
P(A \cup B)
~+~\Bigl[\sum{P(\{\omega_i\})}~\forall \omega_i \in
(A \cap B) \Bigr]}~\color{green}{\text{- - - III}}}
&{} \\
{}&{}
& {~=~}& {\rm{
P(A \cup B)
~+~P(A \cap B)}}
&{} \\
\end{array}$
◼ Remarks:
•
Line marked as I:
In this line,
♦ We replace A by (A-B)∪(A∩B)
♦ We replace B by (B-A)∪(A∩B)
•
Line marked as II:
In this line, there are four terms in the RHS.
This is because, each of the two terms in I, is split into two terms.
•
Line marked as III:
The first three terms in II, are replaced using the result in (2)
4. Let us write the above result again:
P(A) + P(B) = P(A∪B) + P(A∩B)
•
Rearranging the terms, we get:
P(A∪B) = P(A) + P(B) - P(A∩B)
• Thus the formula is proved.
Alternate method:
This can be written in 5 steps:
1. Consider the Venn diagram in fig.16.1 above.
2. Suppose that, we want (A∪B).
•
The union of the following two sets will give A∪B:
(i) Set A, which is (red + blue)
(ii) Set B-A, which is green.
•
So we can write:
A∪B = A ∪ (B-A)
2. Set A and set (B-A) are disjoint sets. So we can apply axiom 3. We get:
P(A∪B) = P(A) + P(B-A)
3. Now consider set B.
•
It is the union of two sets:
(i) Set A∩B, which is blue.
(ii) Set B-A, which is green
•
So we can write:
B = (A∩B) ∪ (B-A)
4. Set (A∩B) and set (B-A) are disjoint sets. So we can apply axiom 3. We get:
P(B) = P(A∩B) + P(B-A)
•
From this we get:
P(B-A) = P(B) – P(A∩B)
5. Substituting this value of P(B-A) in (2), we get:
P(A∪B) = P(A) + P(B) – P(A∩B)
•
Thus the formula is proved.
Let us see an interesting case. It can be written in 3 steps:
1. Consider the two formulas:
(i) P(A∪B) = P(A) + P(B)
•
We obtained this formula from axiom 3. We use this formula when A and B are disjoint sets.
(ii) P(A∪B) = P(A) + P(B) – P(A∩B)
•
We use this formula when A and B are not disjoint sets.
2. However, the second formula can be used even if A and B are disjoint sets. The reason can be explained in 4 steps:
(i) When A and B are disjoint sets, (A∩B) = Φ.
(ii) Substituting this in the second formula, we get:
P(A∪B) = P(A) + P(B) – P(Φ)
(iii) But we have seen result 1 in a previous section (see section 16.4):
P(Φ) = 0
(iv) So we get:
P(A∪B) = P(A) + P(B) – 0
⇒ P(A∪B) = P(A) + P(B)
3. We can write:
The formula in 1(ii) is valid even if A and B are disjoint sets.
In the next section, we will see Probability of event "not A".
No comments:
Post a Comment