In the previous section, we saw range and it's limitations. In this section, we will see mean deviation.
Mean deviation
This can be written in steps:
1. Mean deviation is: “mean (average) of the deviations”.
♦ So first we have to calculate the deviations.
♦ Then we calculate the mean of those deviations.
2. How do we calculate the deviations?
The answer can be written in 3 steps:
(i) First write down the value of the central tendency.
•
The central tendency to be used, can be either mean or median.
•
That central tendency number is represented by the letter ‘a’.
(ii) The values in the data can be represented using the letter ‘x’
•
Pick the first value (x1) in the data. Calculate (x1 - a) for that value.
•
This (x1 - a) is the deviation of the first value.
(iii) In this way, we must calculate the deviation for all values in the data.
3. Once all the deviations are calculated, we must find the sum of those deviations.
•
This sum, when divided by the number of observations (n = ∑fi) will give the mean deviation.
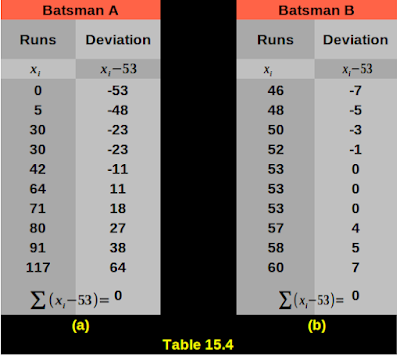
4. Let us calculate the mean deviation for the batsmen A and B.
•
Let us use the mean as the central tendency. So a = 53 for both A and B.
♦ We have to calculate (x-a), which is (x – 53).
♦ We have to calculate this (x-53) for all values.
•
This is shown in table 15.4 (a) and (b) below:
5. Now we encounter a problem. It can be explained in two steps:
(i) We know that, mean deviation = $\frac{\sum{(x_i - 53)}}{\sum{f_i}}$
♦ Where (n = ∑fi) is the number of observations.
(ii) But the sum in the numerator works out to zero for both A and B.
•
So the mean deviation will be zero for both A and B.
6. This situation is not unexpected. If we calculate the deviations in this way, the sum will be zero in all problems. Not just for A and B. The reason can be explained in 4 steps:
(i) In the fig.15.2(a) below, the red bars are the observations in a data. The mean of those observations is the one with the arrow mark.
 |
| Fig.15.2 |
•
We see that:
♦ Some observations are smaller than the mean.
♦ Some observations are larger than the mean.
(ii) In fig.b, the yellow bars are the deviations of those observations which are smaller than the mean. These deviations will be -ve.
(iii) Also in fig.b, the green bars are the deviations of those observations which are larger than the mean. These deviations will be +ve.
(iv) Now we calculate the sum of deviations:
♦ The sum of yellow bars
♦ will be equal to
♦ The sum of green bars.
•
The yellow bars are -ve and green bars are +ve. So the total sum of all deviations will be zero.
7. So we have to apply a modification to the deviation. It can be written in 3 steps:
(i) By the term “deviation”, we are referring to the “difference from the central value”.
(ii) In fig.15.2(b) above, the lengths of the yellow bars are -ve deviations.
•
But “lengths” are “distances”. They do not have signs.
♦ It is the magnitude of those lengths that matters. ♦ There is no need to put the -ve signs.
(iii) So the modification can be applied by taking the absolute values.
•
We can write:
♦ The sum used in the numerator
♦ must be
♦ The sum of absolute values of the deviations.
8. Based on this, we can write the formulas for calculating mean deviation (M.D):
(i) $\text{M.D.(a)}~=~\frac{\sum{(|x_i - a|)}}{\sum{f_i}}$
•
If any observation xi is present more than once, it's frequency is greater than 1. So it is better to apply frequency to all observations in general. So the formula becomes:
$\text{M.D.(a)}~=~\frac{\sum{(f_i |x_i - a|)}}{\sum{f_i}}$
•
In this formula,
♦ "M.D.(a)" indicates that, the mean deviation is taken about the central tendency value "a".
♦ ∑fi is the sum of frequencies, which will give the total number of observations.
(ii) If we decide to use the "mean" as the central tendency value, then "a" will become "$\bar{x}$".
•
So the formula becomes:
$\text{M.D.}(\bar{x})~=~\frac{\sum{(f_i |x_i - \bar{x}|)}}{\sum{f_i}}$
(iii) If we decide to use the "median" as the central tendency value, then "a" will become "M".
•
So the formula becomes:
$\text{M.D.(M)}~=~\frac{\sum{(f_i |x_i - \text{M}|)}}{\sum{f_i}}$
Now we will see some solved examples:
Solved Example 15.1
Find the mean deviation about the mean for the following data:
6,7,10,12,13,4,8,12
Solution:
1. We are asked to find the mean deviation about the mean.
•
So our first aim is to find the mean $(\bar{x})$. For that, we can use the first, second and third columns of table 15.5 below:
 |
| Table 15.5 |
•
Based on those columns, we can write:
$\bar{x}~=~\frac{\sum{f_i x_i}}{\sum{f_i}}~=~\frac{72}{8}~=~9$
2. Now we can calculate the mean deviation. For that, we can use second, fourth and fifth columns of the table.
• We have:
$\text{M.D.}(\bar{x})~=~\frac{\sum{(f_i |x_i - \bar{x}|)}}{\sum{f_i}}$
•
Substituting the values, we get:
$\text{M.D.}(\bar{x})~=~\frac{22}{8}~=~2.75$
Solved Example 15.2
Find the mean deviation about the mean for the following data:
12,3,18,17,4,9,17,19,20,15,8,17,2,3,16,11,3,1,0,5
Solution:
1. We are asked to find the mean deviation about the mean.
•
So our first aim is to find the mean $(\bar{x})$. For that, we can use the first, second and third columns of table 15.6 below:
 |
| Table.15.6 |
•
Based on the table, we can write:
$\bar{x}~=~\frac{\sum{f_i x_i}}{\sum{f_i}}~=~\frac{200}{20}~=~10$
2. Now we can calculate the mean deviation. For that, we can use second, fourth and fifth columns of the table.
• We have:
$\text{M.D.}(\bar{x})~=~\frac{\sum{(f_i |x_i - \bar{x}|)}}{\sum{f_i}}$
•
Substituting the values, we get:
$\text{M.D.}(\bar{x})~=~\frac{124}{20}~=~6.2$
Solved Example 15.3
Find the mean deviation about the median for the following data:
3,9,5,3,12,10,18,4,7,19,21
Solution:
1. We are asked to find the mean deviation about the median.
•
So our first aim is to find the median M. For that, we can use the first, second and third columns of the table 15.7 below. The observations are arranged in ascending order.
 |
| Table 15.7 |
•
Based on the table, we can write:
Total number of observations = n = ∑fi = 11
•
"11" is an odd number. So the position of the median will be:
$\frac{n+1}{2}~=~\frac{11+1}{2}~=~\frac{12}{2}~=~6$
•
From the column for cumulative frequency, we see that, the observation at the sixth position is 9.
•
So we get: M = 9
2. Now we can calculate the mean deviation. For that, we can use second, fourth and fifth columns of the table.
$\text{M.D.(M)}~=~\frac{\sum{(f_i |x_i - M|)}}{\sum{f_i}}$
• Substituting the values, we get:
$\text{M.D.(M)}~=~\frac{58}{11}~=~5.27$
In the next section, we will see a few more solved examples.
No comments:
Post a Comment