In the previous section, we saw some solved examples on how to expand binomials. In this section, we will see General and Middle terms in binomial expansions.
Some basics about general term can be written in 5 steps:
1. In the binomial expansion for (a+b)n, let us denote the position of any term by r. Then:
♦ For the first term, r = 1
♦ For the second term, r = 2
♦ For the third term, r = 3
♦ For the fourth term, r = 4
♦ so on . . .
2. Now let us consider each term of the expansion:
• When r = 1, the term is nC0 an-0 b0
♦ We see that:
✰ The subscript of C is (r-1)
✰ The power of a is [n-(r-1)]
✰ The power of b is (r-1)
• When r = 2, the term is nC1 an-1 b1
♦ We see that:
✰ The subscript of C is (r-1)
✰ The power of a is [n-(r-1)]
✰ The power of b is (r-1)
• When r = 3, the term is nC2 an-2 b2
♦ We see that:
✰ The subscript of C is (r-1)
✰ The power of a is [n-(r-1)]
✰ The power of b is (r-1)
◼ So we see a definite pattern in the subscript of C, power of a and power of b.
3. We see that (r-1) occurs frequently.
• This is inconvenient. We want r instead of (r-1).
• For that, we consider the (r+1)th term instead of the rth term.
4. Let us see the new pattern:
• When r = 1, we get: (r+1) = 2
So we consider the second term, which is: nC1 an-1 b1
♦ We see that:
✰ The subscript of C is r
✰ The power of a is [n-r]
✰ The power of b is r
• When r = 2, we get: (r+1) = 3
So we consider the third term, which is: nC2 an-2 b2
♦ We see that:
✰ The subscript of C is r
✰ The power of a is [n-r]
✰ The power of b is r
• When r = 1, we get: (r+1) = 2
So we consider the second term, which is: nC3 an-3 b3
♦ We see that:
✰ The subscript of C is r
✰ The power of a is [n-r]
✰ The power of b is r
◼ So we get a new pattern in the subscript of C, power of a and power of b. Also, in this pattern, there is no (r-1). Only r.
5. Based on this, we can consider the (r+1)th term as the general term.
• We get: (r+1)th term = nCr an-r br
• The (r+1)th term is denoted as: Tr+1
• So we can write: Tr+1 = nCr an-r br
Some basics about middle term can be written in 8 steps:
1. We know that, if the index is n, then the number of terms will be (n+1)
• Also we know that, if n is even, (n+1) will be odd.
2. So we can write:
If the index n is even, there will be an odd number of terms in the expansion.
• For example, if the index is 6, there will be 7 terms in the expansion.
3. If the number of terms is odd, there will be a unique middle term. An example is shown in fig.8.4 below:
 |
| Fig.8.4 |
• There are a total of 7 terms. There are 3 terms on either sides. The fourth term is the middle term.
4. We can write a relation between the two items below:
♦ The index n
♦ The position of the middle term
• The relation is:
Position of the middle term when the index n is even = $\left(\frac{(n+1)+1}{2} \right)~=~\frac{n+2}{2}~=~\frac{n}{2}+1$
5. Next we will consider the case when n is odd.
• We know that if the index is n, then the number of terms will be (n+1)
• Also we know that if n is odd, (n+1) will be even.
6. So we can write:
If the index n is odd, there will be an even number of terms in the expansion.
• For example, if the index is 7, there will be 8 terms in the expansion.
7. If the number of terms is odd, there will be two middle terms. An example is shown in fig.8.5 below:
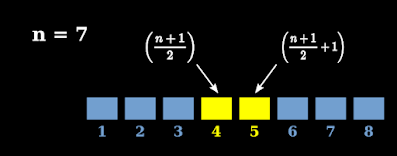 |
| Fig.8.5 |
• There are a total of 8 terms. There are 3 terms on either sides. The fourth and fifth terms are the middle terms.
8. We can write a relation between the two items below:
♦ The index n
♦ The positions of the middle terms
• The relation is:
Positions of the middle terms when the index n is odd = $\frac{n+1}{2}~\text{and}~\frac{n+1}{2}+1$
Now we know how to calculate the position of middle terms. Let us see an interesting case. It can be written in 5 steps:
1. We know that, if n is a natural number, 2n will be an even number.
2. So if the index is 2n, then there will be an odd number (2n+1) of terms.
3. We have seen that, if the number of terms is odd, there will be an unique middle term.
• Based on fig.8.4 above, the position of that middle term is: $\frac{2n}{2}+1~=~(n+1)$
4. Now consider the expansion of $\left(x+ \frac{1}{x} \right)^{2n}$
• We want to find the middle term, which is the (n+1)th term.
• We know that, the (r+1)th term of any binomial expansion is given by: nCr an-r br
5. So in our present case, the middle term, which is the (n+1)th term will be:
${}^{2n} {\rm{C}}_n\;x^{2n-n}\;\left(\frac{1}{x} \right)^n$
${}={}^{2n} {\rm{C}}_n\;x^{n}\;\left(\frac{1}{x} \right)^n$
${}={}^{2n} {\rm{C}}_n$
• This term does not have x. So it is known as: the term independent of x.
• It is also known as the constant term.
Now we will see a solved example.
Solved example 8.5
Find a if the 17th and 18th terms of the expansion (2 + a)50 are equal.
Solution:
1. We have the formula to find the (r+1)th term: : Tr+1 = nCr an-r br
2. Put r = 16. We get:
17th term = ${}^{50} {\rm{C}}_{16} × 2^{50-16} × a^{16}$
= ${}^{50} {\rm{C}}_{16} × 2^{34} × a^{16}$
3. Put r = 17. We get:
18th term = ${}^{50} {\rm{C}}_18 × 2^{50-17} × a^17$
= ${}^{50} {\rm{C}}_17 × 2^{33} × a^17$
4. Given that, the two terms are equal. So we can write:
${}^{50} {\rm{C}}_{16} × 2^{34} × a^{16}~=~{}^{50} {\rm{C}}_{17} × 2^{33} × a^{17}$
• This can be rearranged as: $\frac{{}^{50} {\rm{C}}_{16} × 2^{34}}{{}^{50} {\rm{C}}_{17} × 2^{33}}~=~\frac{a^{17}}{a^{16}}$
$\Rightarrow \frac{{}^{50} {\rm{C}}_{16} × 2}{{}^{50} {\rm{C}}_{17}}~=~a$
• Thus we get: a = 1
In the next section we will see a few more solved examples.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment