In the previous section, we saw the basic details about Pascal's triangle. We saw the necessity for developing a rule to find the various numbers in the Pascal's triangle. In this section, we will see such a rule.
The basics about the rule can be written in 6 steps:
1. We have seen the concept of combination in the previous chapter.
We saw the formula: ${}^n {\rm{C}}_r~=~\frac{n!}{r!(n-r)!}$
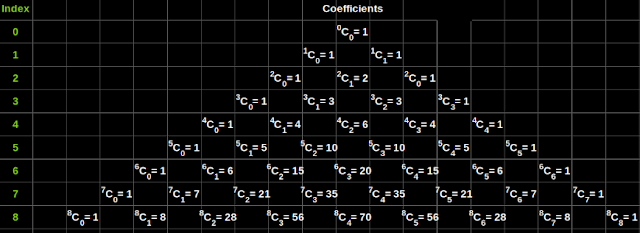
2. Let us check whether this formula is applicable to the Pascal's triangle. The triangle is shown below for easy reference:
 |
| Fig.8.2 |
The check can be done in 3 steps:
(i) Consider any coefficient in the Pascal's triangle, say the fourth coefficient for index 5
♦ The fourth coefficient of index 5 is 10
♦ 5C3 is also 10
(ii) Consider any other coefficient in the Pascal's triangle, say the third coefficient for index 7
♦ The third coefficient of index 7 is 21
♦ 7C2 is also 21
(iii) Let us check one more coefficient in the Pascal's triangle, say the fifth coefficient for index 8
♦ The fifth coefficient of index 8 is 70
♦ 8C4 is also 70
3. This gives us an idea to pick out any coefficient in the Pascal’s triangle:
The xth coefficient for any index n will be nCx-1
• For example, let n be 6 and x be 5
♦ Then the 5th coefficient of index 6 will be be 6C5-1 = 6C4 = 15
♦ From the Pascal's triangle, we see that, this is true.
4. Based on this information, the Pascal’s triangle can be modified as shown in fig.8.3 below:
 |
| Fig.8.3 |
• In the modified triangle, we see two points:
(i) In any row, the subscript on the right side of ‘C’ progressively increases in the order: 0, 1, 2, 3, . . . n
♦ Where n is the index of that row.
(ii) In any row, the superscript on the left side of ‘C’ does not change.
♦ It is equal to n, the index of the row.
5. The above two points give us an idea to quickly write any row of the Pascal’s triangle.
• For example, based on the two points, the row for index 12 will be:
12C0, 12C1, 12C2, 12C3, 12C4, 12C5, 12C6, 12C7, 12C8, 12C9, 12C10, 12C11, 12C12
6. If we can write any row of the Pascal’s triangle quickly, we will be able to write the expansion corresponding to that index also quickly.
• Let us see an example:
Expand (a+b)7
Solution:
1. The coefficients will be:
7C0, 7C1, 7C2, 7C3, 7C4, 7C5, 7C6, and 7C7
2. So the expansion will be:
(a+b)7 =
7C0 a7 + 7C1 a6b1 + 7C2 a5b2 + 7C3 a4b3 + 7C4 a3b4 + 7C5 a2b5 + 7C6 a1b6 + 7C7 b7
• Remember that, the indices of a and b are calculated using the three peculiarities that we wrote in the previous section. They are given below for easy reference:
| (i) The total number of terms in the expansion, is one more than the index. (ii) Powers of the first quantity ‘a’ go on decreasing by 1 whereas the powers of the second quantity ‘b’ increase by 1, in the successive terms. (iii) In each term of the expansion, the sum of the indices of a and b is the same and is equal to the index of (a+b). |
• Thus we can write the complete expansion.
Now we can write the general form. It can be written in 3 steps:
(i) All the coefficients are of the form nCr
♦ For any particular problem, ‘n’ will be a constant.
✰ It will be equal to the index in the question.
♦ r will increase from 0 to n
(ii) The indices of a and b are calculated using the three peculiarities that we wrote in the previous section (also shown in the box above).
(iii) Based on this, the general form will be:
$(a+b)^n~=~{}^n {\rm{C}}_0 a^n~+~{}^n {\rm{C}}_1 a^{n-1} b~+~{}^n {\rm{C}}_2 a^{n-2} b^2~+~{}^n {\rm{C}}_3 a^{n-3} b^3~+~.~.~.~+~{}^n {\rm{C}}_{n-1} a b^{n-1}~+~{}^n {\rm{C}}_n b^n$
• Let us use this general form to expand (2x+5)6
We get:
(2x+5)6
$\begin{array}{ll}
{}={}&{}^6 {\rm{C}}_0 (2x)^6\,5^0
&{}+{}& {}^6 {\rm{C}}_1 (2x)^5\,5^1
&{}+{}& {}^6 {\rm{C}}_2
(2x)^4\,5^2
&{}+{}& {}^6 {\rm{C}}_3 (2x)^3\,5^3
&{}+{}& {}^6 {\rm{C}}_4 (2x)^2\,5^4
&{}+{}& {}^6 {\rm{C}}_5
(2x)^1\,5^5
&{}+{}& {}^6 {\rm{C}}_6 (2x)^0\,5^6 \\
{}={}&{}^6 {\rm{C}}_0
2^6\,x^6\,5^0
&{}+{}& {}^6 {\rm{C}}_1 2^5\,x^5\,5^1
&{}+{}& {}^6 {\rm{C}}_2
2^4\,x^4\,5^2
&{}+{}& {}^6 {\rm{C}}_3 2^3\,x^3\,5^3
&{}+{}& {}^6 {\rm{C}}_4
2^2\,x^2\,5^4
&{}+{}& {}^6 {\rm{C}}_5
2^1\,x^1\,5^5
&{}+{}& {}^6 {\rm{C}}_6 2^0\,x^0\,5^6 \\
{}={}&{}^6 {\rm{C}}_0 × 64 × x^6
× 5^0
&{}+{}& {}^6 {\rm{C}}_1 × 32 × x^5 × 5^1
&{}+{}& {}^6 {\rm{C}}_2 × 16 ×
x^4\,5^2
&{}+{}& {}^6 {\rm{C}}_3 × 8 × x^3 × 5^3
&{}+{}& {}^6 {\rm{C}}_4 × 4 × x^2
× 5^4
&{}+{}& {}^6 {\rm{C}}_5 × 2 × x^1\,5^5
&{}+{}& {}^6 {\rm{C}}_6 × 1 ×
x^0\,5^6 \\
{}={}&1 × 64 × x^6 × 5^0
&{}+{}& 6 × 32 × x^5 × 5^1
&{}+{}& 15 ×
16 × x^4 × 5^2
&{}+{}& 20 × 8 × x^3 × 5^3
&{}+{}& 15 × 4 × x^2 ×
5^4
&{}+{}& 6 × 2 × x^1 × 5^5
&{}+{}& 1 × 1 × x^0 × 5^6 \\
{}={}&1 × 64 × x^6 × 1
&{}+{}& 6 × 32 × x^5 × 5
&{}+{}& 15 ×
16 × x^4 × 25
&{}+{}& 20 × 8 × x^3 × 125
&{}+{}& 15 × 4 × x^2 ×
625
&{}+{}& 6 × 2 × x^1 × 3125
&{}+{}& 1 × 1 × x^0 × 15625 \\
{}={}&64 x^6
&{}+{}& 960 x^5
&{}+{}& 6000 x^4
&{}+{}& 20000 x^3
&{}+{}& 37500 x^2
&{}+{}& 37500 x
&{}+{}& 15625 \\
\end{array}$
We have seen the general form. The RHS of that general form is a bit lengthy. It can be easily shortened as explained by the 4 steps below:
1. We see that, the RHS is a sum of a finite number of terms. So it is a summation.
• We can use the symbol '∑' (Greek upper case letter sigma) to denote summation. Thus the general form becomes:
$(a+b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;a^{n-k}\;b^k}$
2. We know that, for any particular problem, n will be a constant. It is the index.
3. k is not a constant. It takes different values in different terms.
• 'k=0' at the bottom of '∑' indicates that, the value of k starts from zero. In other words, the value of k in the first term is zero.
• 'k=n' at the top of '∑' indicates that, the value of k ends at
n. In other words, the value of k in the last term is n.
• So the values of k are: 0, 1, 2, 3, . . . n
• It is known as the summation from k = 0 to k = n.
4. The index of a is (n-k). The index of b is k.
This shows that, the sum of the indices of a and b will be n in every term.
Let us see some special cases:
Case 1:
In this case, we investigate the expansion when the second quantity is -ve. This can be written in 3 steps:
1. Let us put a = x and b = -y. Then we get:
(a+b)n = (x-y)n = [x + (-y)]n
2. Expanding this using the general form, we get:
$[x+(-y)]^n$
$\begin{array}{ll}
{}={}&{}^n {\rm{C}}_0 \,x^n\,(-y)^0
&{}+{}& {}^n
{\rm{C}}_1\, x^{n-1}\,(-y)^1
&{}+{}& {}^n {\rm{C}}_2 \,x^{n-2}\,(-y)^2
&{}+{}& {}^n
{\rm{C}}_3\, x^{n-3}\,(-y)^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\,
x^0\,(-y)^n&{}& {} &{} \\
{}={}&{}^n {\rm{C}}_0 \,x^n\,(-1)^0\,y^0
&{}+{}& {}^n {\rm{C}}_1\,
x^{n-1}\,(-1)^1\,y^1
&{}+{}& {}^n {\rm{C}}_2 \,x^{n-2}\,(-1)^2\,y^2
&{}+{}& {}^n {\rm{C}}_3\,
x^{n-3}\,(-1)^3\,y^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, x^0\,(-1)^n\,y^n&{}& {}
&{} \\
\end{array}$
$~{}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, x^{n-k}\;y^k}$
3. Based on the above result, we can write:
$(a-b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, a^{n-k}\;b^k}$
◼ Let us expand (x-2y)5 using this result. We get:
$(x-2y)^5~=~[x+(-2y)]^5~=~\sum\limits_{k\,=\,0}^{k\,=\,5}{{}^5 {\rm{C}}_k\;(-1)^k \, x^{6-k}\;(-2y)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(x-2y)^5$
$\begin{array}{ll}
{}={}&{}^5 {\rm{C}}_0 \,x^5\,(-1)^0\,(2y)^0
&{}+{}& {}^5 {\rm{C}}_1\,
x^{5-1}\,(-1)^1\,(2y)^1
&{}+{}& {}^5 {\rm{C}}_2 \,x^{5-2}\,(-1)^2\,(2y)^2
&{}+{}& {}^5 {\rm{C}}_3\,
x^{5-3}\,(-1)^3\,(2y)^3
&{}+{}& {}^5 {\rm{C}}_4\,
x^{5-4}\,(-1)^4\,(2y)^4
&{}+{}& {}^5 {\rm{C}}_5\,
x^{5-5}\,(-1)^5\,(2y)^5&{}& {}
&{} \\
{}={}&1 × x^5 × 1 × (2y)^0
&{}+{}& 5 ×
x^4 × -1 × (2y)
&{}+{}& 10 ×
x^3 × 1 × (4y^2)
&{}+{}& 10 ×
x^2 × -1 × (8y^3)
&{}+{}& 5 ×
x^1 × 1 × (16y^4)
&{}+{}& 1 ×
x^0 × -1 × (32y^5) \\
{}={}&x^5
&{}-{}& 10x^4 y
&{}+{}& 40x^3 y^2
&{}-{}& 80
x^2 y^3
&{}+{}& 80 x y^4
&{}-{}& 32y^5 \\
\end{array}$
Case 2:
In this case, we investigate the expansion when the first quantity is 1. This can be written in 3 steps:
1. Let us put a = 1 and b = x. Then we get:
(a+b)n = (1+x)n
2. Expanding this using the general form, we get:
$(1+x)^n$
$\begin{array}{ll}
{}={}&{}^n {\rm{C}}_0 \,1^n\,x^0
&{}+{}& {}^n
{\rm{C}}_1\, 1^{n-1}\,x^1
&{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,x^2
&{}+{}& {}^n
{\rm{C}}_3\, 1^{n-3}\,x^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\,
1^0\,x^n&{}& {} &{} \\
{}={}&{}^n {\rm{C}}_0 \,1^n\,x^0
&{}+{}& {}^n {\rm{C}}_1\,
1^{n-1}\,x^1
&{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,x^2
&{}+{}& {}^n {\rm{C}}_3\,
1^{n-3}\,x^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,x^n&{}& {}
&{} \\
\end{array}$
${}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\, 1^{n-k}\;x^k}$
3. So we can write:
$(1+x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;x^k}$
◼ Let us expand (1+2x)6 using this result. We get:
$(1+2x)^6~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^6 {\rm{C}}_k\;(2x)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(1+2x)^6$
$\begin{array}{ll}
{}={}&{}^6 {\rm{C}}_0 \,1^6\,(2x)^0
&{}+{}& {}^6 {\rm{C}}_1\,(2x)^1
&{}+{}& {}^6 {\rm{C}}_2\,(2x)^2
&{}+{}& {}^6 {\rm{C}}_3\,(2x)^3
&{}+{}& {}^6 {\rm{C}}_4\,(2x)^4
&{}+{}& {}^6 {\rm{C}}_5\,(2x)^5
&{}+{}& {}^6 {\rm{C}}_6\,(2x)^6&{}& {}
&{} \\
{}={}&1 × (2x)^0
&{}+{}& 6 × (2x)
&{}+{}& 15 × (4x^2)
&{}+{}& 20 × (8x^3)
&{}+{}& 15 × (16x^4)
&{}+{}& 6 × (32x^5)
&{}+{}& 1 × (64x^6) \\
{}={}&1
&{}+{}& 12x
&{}+{}& 60 x^2
&{}+{}& 160 x^3
&{}+{}& 240 x^4
&{}+{}& 192 x^5
&{}+{}& 64x^6 \\
\end{array}$
◼ x = 1 is a special case coming under this category. We get:
$(1+x)^n~=~(1+1)^n~=~2^n~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k\;x^k}~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k\;1^k}~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
${}={}~{}^n {\rm{C}}_0
~+~{}^n
{\rm{C}}_1
~+~{}^n {\rm{C}}_2
~+~{}^n
{\rm{C}}_3
~+~.~.~.~+~{}^n {\rm{C}}_n$
• So we can write:
$2^n~=~{}^n {\rm{C}}_0
~+~{}^n
{\rm{C}}_1
~+~{}^n {\rm{C}}_2
~+~{}^n
{\rm{C}}_3
~+~.~.~.~+~{}^n {\rm{C}}_n$
Case 3:
In this case, we investigate the expansion when the first quantity is 1 and the second quantity is -ve. This can be written in 3 steps:
1. Let us put a = 1 and b = -x. Then we get:
(a+b)n = (1-x)n = [1 + (-x)]n
2. Expanding this using the general form, we get:
$[1+(-x)]^n$
$\begin{array}{ll}
{}={}&{}^n {\rm{C}}_0 \,1^n\,(-x)^0
&{}+{}& {}^n
{\rm{C}}_1\, 1^{n-1}\,(-x)^1
&{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,(-x)^2
&{}+{}& {}^n
{\rm{C}}_3\, 1^{n-3}\,(-x)^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\,
1^0\,(-x)^n&{}& {} &{} \\
{}={}&{}^n {\rm{C}}_0 \,1^n\,(-1)^0\,x^0
&{}+{}& {}^n {\rm{C}}_1\,
1^{n-1}\,(-1)^1\,x^1
&{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,(-1)^2\,x^2
&{}+{}& {}^n {\rm{C}}_3\,
1^{n-3}\,(-1)^3\,x^3
&{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,(-1)^n\,x^n&{}& {}
&{} \\
\end{array}$
${}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, 1^{n-k}\;x^k}$
3. Based on the above result, we can write:
$(1-x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;x^k}$
◼ Let us expand (1-2x)5 using this result. We get:
$(1-2x)^5~=~[1+(-2x)]^5~=~\sum\limits_{k\,=\,0}^{k\,=\,5}{{}^5 {\rm{C}}_k\;(-1)^k\;(-2x)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(1-2x)^5$
$\begin{array}{ll}
{}={}&{}^5 {\rm{C}}_0\,(-1)^0\,(2x)^0
&{}+{}& {}^5 {\rm{C}}_1\,(-1)^1\,(2x)^1
&{}+{}& {}^5 {\rm{C}}_2\,(-1)^2\,(2x)^2
&{}+{}& {}^5 {\rm{C}}_3\,(-1)^3\,(2x)^3
&{}+{}& {}^5 {\rm{C}}_4\,(-1)^4\,(2x)^4
&{}+{}& {}^5 {\rm{C}}_5\,(-1)^5\,(2x)^5&{}& {}
&{} \\
{}={}&1 × 1 × (2x)^0
&{}+{}& 5 × -1 × (2x)
&{}+{}& 10 × 1 × (4x^2)
&{}+{}& 10 × -1 × (8x^3)
&{}+{}& 5 × 1 × (16x^4)
&{}+{}& 1 × -1 × (32x^5) \\
{}={}&1
&{}-{}& 10 x
&{}+{}& 40 x^2
&{}-{}& 80 x^3
&{}+{}& 80 x^4
&{}-{}& 32 x^5 \\
\end{array}$
• We wrote: $(1-x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;x^k}$
◼ x = 1 is a special case coming under this category. We get:
$(1-x)^n~=~(1-1)^n~=~0^n
~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;1^k}
~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k }$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
${}={}~{}^n {\rm{C}}_0\;(-1)^0
~+~{}^n
{\rm{C}}_1\;(-1)^1
~+~{}^n {\rm{C}}_2\;(-1)^2
~+~{}^n
{\rm{C}}_3
~+~.~.~.~+~{}^n {\rm{C}}_n\;(-1)^n$
• So we can write:
$0^n~=~{}^n {\rm{C}}_0
~-~{}^n
{\rm{C}}_1
~+~{}^n {\rm{C}}_2
~-~{}^n
{\rm{C}}_3
~+~.~.~.~+~(-1)^n~ × ~{}^n {\rm{C}}_n$
In the next section we will see some solved examples.
Copyright©2022 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment