Chapter 8.4 - Solved Examples on General and Middle Terms

In the previous section, we saw General and Middle terms in binomial expansions. We saw a solved example also. In this section, we will see a few more solved examples.

Solved example 8.6
Show that the middle term in the expansion of $(1+x)^{2n}$ is $\frac{1 × 3 × 5~.~.~.~(2n-1)}{n!} 2n x^n$, where n is a positive integer.
Solution:
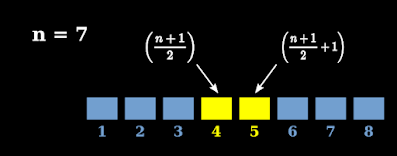
1. Given that, n is a +ve integer. So 2n will be an even number.
2. Since the index is 2n, there will be an odd number (2n+1) of terms.
3. We have seen that, if the number of terms is odd, there will be an unique middle term.
• It's position is given by: $\frac{2n}{2}+1~=~(n+1)$
4. Now consider the expansion of $(1+x)^{2n}$
• We want to find the middle term, which is the (n+1)^th term.
• We know that, the (r+1)^th term of the binomial expansion (a+b)ⁿ is given by: ⁿC_r a^n-r b^r
5. In our present case, a = 1, b = x and n = 2n.
So the middle term, which is the (n+1)^th term will be:
${}^{2n} {\rm{C}}_n\;1^{2n-n}\;x^n$
$\begin{array}{ll} {}={}&{}^{2n} {\rm{C}}_n\; × 1 × x^n&{}& {} &{} \\ {}={}&\frac{2n! × x^n}{n!(2n-n)!}&{}& {} &{} \\ {}={}&\frac{2n! × x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{2n(2n-1)(2n-2)~.~.~.~4 × 3 × 2 × 1 × x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{1 × 2 × 3 × 4~.~.~.~(2n-2)(2n-1)2n× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{1 × 2 × 3 × 4~.~.~.~(2n-1)2n× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{[1 × 3 × 5 × ~.~.~.~ ×(2n-1)] [2 × 4 × 6 × ~.~.~.~ × 2n]× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{[1 × 3 × 5 × ~.~.~.~ ×(2n-1)] [(2 × 1) × (2 × 2) × (2 × 3) × ~.~.~.~ × (2 × n)]× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{[1 × 3 × 5 × ~.~.~.~ ×(2n-1)] 2^n[1 × 2 × 3 × ~.~.~.~ × n]× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{[1 × 3 × 5 × ~.~.~.~ ×(2n-1)] 2^n[n!]× x^n}{n! n!}&{}& {} &{} \\ {}={}&\frac{[1 × 3 × 5 × ~.~.~.~ ×(2n-1)] 2^n× x^n}{n!}&{}& {} &{} \\ \end{array}$

Solved example 8.7
Find the coefficient of x⁶y³ in the expansion of (x+2y)⁹
Solution:
1. Assume that x⁶y³ occurs in the (r+1)^th term.
• We know that, the (r+1)^th term of the binomial expansion (a+b)ⁿ is given by: ⁿC_r a^n-r b^r
• In our present case, n = 9, a = x and b = 2y
2. So we can write:
(r+1)^th term of the expansion of (x+2y)⁹ = ⁹C_r x^9-r (2y)^r
= ⁹C_r x^9-r 2^r y^r = [⁹C_r  × 2^r][x^9-r  × y^r]
• Thus we get:
   ♦ Constant part (coefficient) of the (r+1)^th term  = [⁹C_r  × 2^r]
   ♦ Variable part of the (r+1)^th term = [x^9-r  × y^r]
3. But given that, the variable part is x⁶y³
Comparing this with [x^9-r  × y^r], we get: r = 3
4. So the coefficient = [⁹C_r  × 2^r] = [⁹C₃  × 2³] = 672

Solved example 8.8
The second, third and fourth terms in the binomial expansion (x + a)ⁿ are
240, 720 and 1080, respectively. Find x, a and n.
Solution:
1. We know that, the (r+1)^th term of the binomial expansion (a+b)ⁿ is given by: ⁿC_r a^n-r b^r
• In our present case, a = x and b = a
2. For the second term, r = 1
So we get: T₂ = ⁿC₁ x^n-1 a¹ = 240  
3. For the third term, r = 2
So we get: T₃ = ⁿC₂ x^n-2 a² = 720  
4. For the fourth term, r = 3
So we get: T₄ = ⁿC₃ x^n-3 a³ = 1080
5. Dividing (3) by (2), we get:
$\begin{array}{ll} {\frac{T_3}{T_2}}&{}={} &\frac{{}^{n} {\rm{C}}_2 × x^{n-2} × a^2}{{}^{n} {\rm{C}}_1 × x^{n-1} × a^1}& {}={} &\frac{720}{240}& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{{}^{n} {\rm{C}}_2 × x^n × x^{-2} × a^2}{{}^{n} {\rm{C}}_1 × x^n × x^{-1} × a^1}}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{{}^{n} {\rm{C}}_2 × x^{-1} × a}{{}^{n} {\rm{C}}_1 }}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{\frac{n!}{2!(n-2)!} × x^{-1} × a}{\frac{n!}{1!(n-1)!} }}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{1!(n-1)! × x^{-1} × a}{2!(n-2)! }}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{(n-1)(n-2)! × x^{-1} × a}{2 × (n-2)! }}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{(n-1) × x^{-1} × a}{2}}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{(n-1)}{2}~ × ~\frac{a}{x}}& {}={} &3& {} &{}& {} &{}& {}&{}& {} &{} \\ \end{array}$

$\Rightarrow~\frac{a}{x}~=~\frac{6}{(n-1)}$ 
6. Dividing (4) by (3), we get:
$\begin{array}{ll} {\frac{T_4}{T_3}}&{}={} &\frac{{}^{n} {\rm{C}}_3 × x^{n-3} × a^3}{{}^{n} {\rm{C}}_2 × x^{n-2} × a^2}& {}={} &\frac{1080}{720}& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{{}^{n} {\rm{C}}_3 × x^n × x^{-3} × a^3}{{}^{n} {\rm{C}}_2 × x^n × x^{-2} × a^2}}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{{}^{n} {\rm{C}}_3 × x^{-1} × a}{{}^{n} {\rm{C}}_2 }}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{\frac{n!}{3!(n-3)!} × x^{-1} × a}{\frac{n!}{2!(n-2)!} }}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{2!(n-2)! × x^{-1} × a}{3!(n-3)! }}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{2! × (n-2)(n-3)! × x^{-1} × a}{3 × 2! × (n-3)! }}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{(n-2) × x^{-1} × a}{3}}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ {}&{}={} &{\frac{(n-2)}{3}~ × ~\frac{a}{x}}& {}={} &1.5& {} &{}& {} &{}& {}&{}& {} &{} \\ \end{array}$
$\Rightarrow~\frac{a}{x}~=~\frac{4.5}{(n-2)}$
7. Equating the results in (5) and (6), we get:
$\frac{a}{x}~=~\frac{6}{(n-1)}~=~\frac{4.5}{n-2}$
$\Rightarrow~6n-12~=~4.5n-4.5$ 
$\Rightarrow~ 1.5n~=~7.5$
$\Rightarrow~ n ~=~5$
8. Substituting the value of n in (5), we get:
$\frac{a}{x}~=~\frac{6}{5-1}~=~\frac{6}{4}~=~1.5$
$\Rightarrow~a~=~1.5x$
9. Substituting the value of n in (2), we get:
⁵C₁ x^5-1 a¹ = 240  
⇒ 5 × x⁴× a = 240
• Substituting for a using (8), we get:
5 × x⁴ × 1.5x = 240
⇒ 7.5x⁵ = 240
⇒ x = 2
10. Substituting for x in (8), we get:
a = 1.5 × 2 = 3

Solved example 8.9
The coefficients of three consecutive terms in the expansion of (1 + a)ⁿ are in the ratio 1: 7 : 42. Find n.
Solution:
1. Let the three consecutive terms be (r+1)^th, (r+2)^th and (r+3)^th
2. The general term is given by: T_r+1 = ⁿC_r a^n-r b^r
• In our present case, a = 1 and b = a
3. The first of the three consecutive terms will be: ⁿC_r+1 1^n-1 a^r+1 = ⁿC_r+1 a^r+1
So the coefficient of this first term will be ⁿC_r+1
4. The second of the three consecutive terms will be: ⁿC_r+2 1^n-2 a^r+2 = ⁿC_r+2 a^r+2
So the coefficient of this second term will be ⁿC_r+2
5. The third of the three consecutive terms will be: ⁿC_r+3 1^n-3 a^r+3 = ⁿC_r+3 a^r+3
So the coefficient of this third term will be ⁿC_r+3
6. We are given the ratio between the coefficients. So we can write:
ⁿC_r+1 : ⁿC_r+2 : ⁿC_r+3 = 1 : 7 : 42
7. Consider the ratio of second coefficient to first coefficient. We get:
$\frac{{}^{n} {\rm{C}}_{r+2}}{{}^{n} {\rm{C}}_{r+1}}~=~7$

$\Rightarrow~\frac{\frac{n!}{(r+2)![n-(r+2)]!}}{\frac{n!}{(r+1)![n-(r+1)]!}}~=~7$

$\Rightarrow~\frac{(r+1)![n-(r+1)]!}{(r+2)![n-(r+2)]!}~=~7$

$\Rightarrow~\frac{(r+1)![n-(r+1)]!}{(r+2)(r+1)![n-(r+2)]!}~=~7$

$\Rightarrow~\frac{[n-(r+1)]!}{(r+2)[n-(r+2)]!}~=~7$

$\Rightarrow~\frac{[n-r-1]!}{(r+2)[n-r-2]!}~=~7$

$\Rightarrow~\frac{[n-r-1][n-r-2]!}{(r+2)[n-r-2]!}~=~7$

$\Rightarrow~\frac{[n-r-1]}{(r+2)}~=~7$

$\Rightarrow~n-r-1~=~7r+14$

$\Rightarrow~n-8r~=~15$

8. Consider the ratio of third coefficient to second coefficient. We get:
$\frac{{}^{n} {\rm{C}}_{r+3}}{{}^{n} {\rm{C}}_{r+2}}~=~\frac{42}{7}~=~6$

$\Rightarrow~\frac{\frac{n!}{(r+3)![n-(r+3)]!}}{\frac{n!}{(r+2)![n-(r+2)]!}}~=~7$

$\Rightarrow~\frac{(r+2)![n-(r+2)]!}{(r+3)![n-(r+3)]!}~=~6$

$\Rightarrow~\frac{(r+2)![n-(r+2)]!}{(r+3)(r+2)![n-(r+3)]!}~=~6$

$\Rightarrow~\frac{[n-(r+2)]!}{(r+3)[n-(r+3)]!}~=~6$

$\Rightarrow~\frac{[n-r-2]!}{(r+3)[n-r-3]!}~=~6$

$\Rightarrow~\frac{[n-r-2][n-r-3]!}{(r+3)[n-r-3]!}~=~6$

$\Rightarrow~\frac{[n-r-2]}{(r+3)}~=~6$

$\Rightarrow~n-r-2~=~6r+18$

$\Rightarrow~n-7r~=~20$

9. So we have two equations:
(i) From (7), we have: n-8r = 15
(ii) From (8), we have: n-7r = 20
Solving these two equations, we get: r = 5 and n = 55

---

The link below gives some more solved examples.

Exercise 8.2

---

In the next section we will see some miscellaneous examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 8.3 - General and Middle Terms

In the previous section, we saw some solved examples on how to expand binomials. In this section, we will see General and Middle terms in binomial expansions.

Some basics about general term can be written in 5 steps:
1. In the binomial expansion for (a+b)ⁿ, let us denote the position of any term by r. Then:
   ♦ For the first term, r = 1   
   ♦ For the second term, r = 2   
   ♦ For the third term, r = 3   
   ♦ For the fourth term, r = 4
   ♦ so on . . .
2. Now let us consider each term of the expansion:
• When r = 1, the term is ⁿC₀ a^n-0 b⁰
   ♦ We see that:
         ✰ The subscript of C is (r-1)
         ✰ The power of a is [n-(r-1)]
         ✰ The power of b is (r-1) 
• When r = 2, the term is ⁿC₁ a^n-1 b¹
   ♦ We see that:
         ✰ The subscript of C is (r-1)
         ✰ The power of a is [n-(r-1)]
         ✰ The power of b is (r-1) 
• When r = 3, the term is ⁿC₂ a^n-2 b²
   ♦ We see that:
         ✰ The subscript of C is (r-1)
         ✰ The power of a is [n-(r-1)]
         ✰ The power of b is (r-1)
◼ So we see a definite pattern in the subscript of C, power of a and power of b.
3. We see that (r-1) occurs frequently.
• This is inconvenient. We want r instead of (r-1).
• For that, we consider the (r+1)^th term instead of the r^th term.
4. Let us see the new pattern:
• When r = 1, we get: (r+1) = 2
So we consider the second term, which is: ⁿC₁ a^n-1 b¹
   ♦ We see that:
         ✰ The subscript of C is r
         ✰ The power of a is [n-r]
         ✰ The power of b is r   
• When r = 2, we get: (r+1) = 3
So we consider the third term, which is: ⁿC₂ a^n-2 b²
   ♦ We see that:
         ✰ The subscript of C is r
         ✰ The power of a is [n-r]
         ✰ The power of b is r   
• When r = 1, we get: (r+1) = 2
So we consider the second term, which is: ⁿC₃ a^n-3 b³
   ♦ We see that:
         ✰ The subscript of C is r
         ✰ The power of a is [n-r]
         ✰ The power of b is r
◼ So we get a new pattern in the subscript of C, power of a and power of b. Also, in this pattern, there is no (r-1). Only r.
5. Based on this, we can consider the (r+1)^th term as the general term.
• We get: (r+1)^th term = ⁿC_r a^n-r b^r
• The (r+1)^th term is denoted as: T_r+1
• So we can write: T_r+1 = ⁿC_r a^n-r b^r

---

Some basics about middle term can be written in 8 steps:
1. We know that, if the index is n, then the number of terms will be (n+1)
• Also we know that, if n is even, (n+1) will be odd.
2. So we can write:
If the index n is even, there will be an odd number of terms in the expansion.
• For example, if the index is 6, there will be 7 terms in the expansion.
3. If the number of terms is odd, there will be a unique middle term. An example is shown in fig.8.4 below:

Fig.8.4

• There are a total of 7 terms. There are 3 terms on either sides. The fourth term is the middle term.
4. We can write a relation between the two items below:
   ♦ The index n
   ♦ The position of the middle term
• The relation is:
Position of the middle term when the index n is even = $\left(\frac{(n+1)+1}{2} \right)~=~\frac{n+2}{2}~=~\frac{n}{2}+1$
5. Next we will consider the case when n is odd.
• We know that if the index is n, then the number of terms will be (n+1)
• Also we know that if n is odd, (n+1) will be even.
6. So we can write:
If the index n is odd, there will be an even number of terms in the expansion.
• For example, if the index is 7, there will be 8 terms in the expansion.
7. If the number of terms is odd, there will be two middle terms. An example is shown in fig.8.5 below:

Fig.8.5

• There are a total of 8 terms. There are 3 terms on either sides. The fourth and fifth terms are the middle terms.
8. We can write a relation between the two items below:
   ♦ The index n
   ♦ The positions of the middle terms
• The relation is:
Positions of the middle terms when the index n is odd = $\frac{n+1}{2}~\text{and}~\frac{n+1}{2}+1$

---

Now we know how to calculate the position of middle terms. Let us see an interesting case. It can be written in 5 steps:
1. We know that, if n is a natural number, 2n will be an even number.
2. So if the index is 2n, then there will be an odd number (2n+1) of terms.
3. We have seen that, if the number of terms is odd, there will be an unique middle term.
• Based on fig.8.4 above, the position of that middle term is: $\frac{2n}{2}+1~=~(n+1)$
4. Now consider the expansion of $\left(x+ \frac{1}{x} \right)^{2n}$
• We want to find the middle term, which is the (n+1)^th term.
• We know that, the (r+1)^th term of any binomial expansion is given by: ⁿC_r a^n-r b^r
5. So in our present case, the middle term, which is the (n+1)^th term will be:
${}^{2n} {\rm{C}}_n\;x^{2n-n}\;\left(\frac{1}{x} \right)^n$   
${}={}^{2n} {\rm{C}}_n\;x^{n}\;\left(\frac{1}{x} \right)^n$   
${}={}^{2n} {\rm{C}}_n$
• This term does not have x. So it is known as: the term independent of x.
• It is also known as the constant term.

Now we will see a solved example.

Solved example 8.5
Find a if the 17^th and 18^th terms of the expansion (2 + a)⁵⁰ are equal.
Solution:
1. We have the formula to find the (r+1)^th term: : T_r+1 = ⁿC_r a^n-r b^r
2. Put r = 16. We get:
17^th term = ${}^{50} {\rm{C}}_{16} × 2^{50-16} × a^{16}$   
= ${}^{50} {\rm{C}}_{16} × 2^{34} × a^{16}$   
3. Put r = 17. We get:
18^th term = ${}^{50} {\rm{C}}_18 × 2^{50-17} × a^17$   
= ${}^{50} {\rm{C}}_17 × 2^{33} × a^17$
4. Given that, the two terms are equal. So we can write:
${}^{50} {\rm{C}}_{16} × 2^{34} × a^{16}~=~{}^{50} {\rm{C}}_{17} × 2^{33} × a^{17}$
• This can be rearranged as: $\frac{{}^{50} {\rm{C}}_{16} × 2^{34}}{{}^{50} {\rm{C}}_{17} × 2^{33}}~=~\frac{a^{17}}{a^{16}}$       
$\Rightarrow \frac{{}^{50} {\rm{C}}_{16} × 2}{{}^{50} {\rm{C}}_{17}}~=~a$
• Thus we get: a = 1

---

In the next section we will see a few more solved examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 8.2 - Binomial Expansion - Solved Examples

In the previous section, we saw how to expand binomials by applying the general form of the binomial theorem. In this section, we will see some solved examples.

Solved example 8.1
Expand $\left(x^2+ \frac{3}{x} \right)^4, ~x \ne 0$ using binomial theorem
Solution:
1. We have: $(a+b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;a^{n-k}\;b^k}$
2. In our present case, $a=x^2,~b=\frac{3}{x}~\rm{and}~n=4$
So we can write:
$\left(x^2+ \frac{3}{x} \right)^4~=~\sum\limits_{k\,=\,0}^{k\,=\,4}{{}^4 {\rm{C}}_k\;\left(x^2 \right)^{4-k}\;\left(\frac{3}{x} \right)^k}$
3. Thus we get:
$\left(x^2+ \frac{3}{x} \right)^4$
$\begin{array}{ll} {}={}&{}^4 {\rm{C}}_0 \,\left(x^2 \right)^4\,\left(\frac{3}{x} \right)^0 &{}+{}& {}^4 {\rm{C}}_1\, \left(x^2 \right)^{4-1}\,\left(\frac{3}{x} \right)^1 &{}+{}& {}^4 {\rm{C}}_2\,\left(x^2 \right)^{4-2}\,\left(\frac{3}{x} \right)^2 &{}+{}& {}^4 {\rm{C}}_3\, \left(x^2 \right)^{4-3}\,\left(\frac{3}{x} \right)^3 &{}+{}& {}^4 {\rm{C}}_4\, \left(x^2 \right)^{4-4}\,\left(\frac{3}{x} \right)^4 \\ {}={}&1 × \left(x^2 \right)^4 × \left(\frac{3}{x} \right)^0 &{}+{}& 4 × \left(x^2 \right)^3 × \left(\frac{3}{x} \right)^1 &{}+{}& 6 × \left(x^2 \right)^2 × \left(\frac{3}{x} \right)^2 &{}+{}& 4 × \left(x^2 \right)^1 × \left(\frac{3}{x} \right)^3 &{}+{}& 1 × \left(x^2 \right)^0 × \left(\frac{3}{x} \right)^4 \\ {}={}&x^8 &{}+{}& 12 x^5 &{}+{}& 54 x^2 &{}+{}& \frac{108}{x} &{}+{}& \frac{81}{x^4} \\ \end{array}$

Solved example 8.2
Compute 98⁵
Solution:
1. First we write 98 as the sum or difference of two numbers.
• Those two numbers must be such that, their powers are easy to calculate.
• So we write: 98 = (100 - 2)
    ♦ Powers of 100 can be easily calculated.
    ♦ Powers of 2 can also be easily calculated.
2. Now we can write:
$98^5~=~(100-2)^5$
3. For expanding this, we can use the formula:
$(a-b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, a^{n-k}\;b^k}$
4. Thus we get:
$(100-2)^5$
$\begin{array}{ll} {}={}&{}^5 {\rm{C}}_0 \,100^5\,(-1)^0\,2^0 &{}+{}& {}^5 {\rm{C}}_1 × 100^{5-1} × (-1)^1 × 2^1 &{}+{}& {}^5 {\rm{C}}_2 × 100^{5-2} × (-1)^2 × 2^2 &{}+{}& {}^5 {\rm{C}}_3 × 100^{5-3} × (-1)^3 × 2^3 &{}+{}& {}^5 {\rm{C}}_4 × 100^{5-4} × (-1)^4 × 2^4 &{}+{}& {}^5 {\rm{C}}_5 × 100^{5-5} × (-1)^5 × 2^5&{}& {} &{} \\ {}={}&1 × 10^{10} × 1 × 1 &{}+{}& 5 × 10^8 × -1 × 2 &{}+{}& 10 × 10^6 × 1 × 4 &{}+{}& 10 × 10^4 × -1 × 8 &{}+{}& 5 × 10^2 × 1 × 16 &{}+{}& 1 × 100^0 × -1 × 32 \\ {}={}&1 × 10^{10} × 1 &{}-{}& 5 × 10^8 × 2 &{}+{}& 10 × 10^6 × 4 &{}-{}& 10 × 10^4 × 8 &{}+{}& 5 × 10^2 × 16 &{}-{}& 1 × 100^0 × 32 \\ {}={}&9039207968 \\ \end{array}$

Solved example 8.3
Which is larger (1.01)^1000000 or 10000 ?
Solution:
1. First we must find (1.01)^1000000. For that, we write 1.01 as the sum or difference of two numbers.
• Those two numbers must be such that, their powers are easy to calculate.
• So we write: 1.01 = (1 + 0.01)
    ♦ Powers of 1 can be easily calculated.
    ♦ Powers of 0.01 can also be easily calculated.
2. Now we can write:
$(1.01)^{1000000}~=~(1+0.01)^{1000000}$
3. For expanding this, we can use the formula:
$(1+x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;x^k}$
4. Thus we get:
$(1+0.01)^{1000000}$
$\begin{array}{ll} {}={}&{}^{1000000} {\rm{C}}_0 × (0.01)^0 &{}+{}& {}^{1000000} {\rm{C}}_1 × (0.01)^1 &{}+{}& {}^{1000000} {\rm{C}}_2 × (0.01)^2 &{}+{}& {}^{1000000} {\rm{C}}_3 × (0.01)^3 &{}+{}& .~.~. &{}+{}& {}^{1000000} {\rm{C}}_{1000000} × (0.01)^{1000000} \\ {}={}&1 × 1 &{}+{}& 1000000 × 0.01 &{}+{}& \text{[a +ve term]} &{}+{}& \text{[a +ve term]} &{}+{}& .~.~. &{}+{}& \text{[a +ve term]} \\ {}={}&1 &{}+{}& 10000 &{}+{}& \text{[a +ve term]} &{}+{}& \text{[a +ve term]} &{}+{}& .~.~. &{}+{}& \text{[a +ve term]} \\ {}={}&10001 &{}+{}& \text{[+ve terms]} \\ \end{array}$
5. 10001 + [+ve terms] will be greater than 10000
• So (1.01)^1000000 is greater than 10000
6. Note that, all terms within the square brackets must be +ve terms. Otherwise there is no guarantee that 10001 + [+ve terms] will be greater than 10000

Solved example 8.4
Using binomial theorem, prove that 6ⁿ – 5n always leaves remainder 1 when divided by 25.
Solution:
1. Let a and b be two natural numbers.
• Suppose that, when a is divided by b, the quotient is q and remainder is r.
• Then we will be able to write: a = bq + r
    ♦ Where q and r are natural numbers.
2. In a similar way,
• If 6ⁿ – 5n, when divided by 25, gives quotient m and remainder 1, we will be able to write: 6ⁿ – 5n = 25m + 1, where m is a natural number.
• So our task is to prove that, 6ⁿ – 5n is equal to 25m + 1
3. We have the formula:
$(1+x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;x^k}$
Put x = 5. Then we get:
$(1+5)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;5^k}$
4. Thus we get:
$(1+5)^n~=~6^n$
$\begin{array}{ll} {}={}&{}^n {\rm{C}}_0 × 5^0 &{}+{}& {}^n {\rm{C}}_1 × 5^1 &{}+{}& {}^n {\rm{C}}_2 × 5^2 &{}+{}& {}^n {\rm{C}}_3 × 5^3 &{}+{}& .~.~. &{}+{}& {}^n {\rm{C}}_n × 5^4 \\ {}={}&1 × 1 &{}+{}& n × 5 &{}+{}& {}^n {\rm{C}}_2 × 5^2 &{}+{}& {}^n {\rm{C}}_3 × 5^3 &{}+{}& .~.~. &{}+{}& {}^n {\rm{C}}_n × 5^4 \\ {}={}&1 &{}+{}& 5n &{}+{}& {}^n {\rm{C}}_2 × 5^2 &{}+{}& {}^n {\rm{C}}_3 × 5^3 &{}+{}& .~.~. &{}+{}& {}^n {\rm{C}}_n × 5^n \\ \end{array}$
5. We can write:
$6^n~=~1~+~5n~+~{}^n {\rm{C}}_2 × 5^2~+~{}^n {\rm{C}}_3 × 5^3 ~+~.~.~.~+~{}^n {\rm{C}}_n × 5^n$
• This can be rearranged as:
$6^n-5n~=~1~+~{}^n {\rm{C}}_2 × 5^2~+~{}^n {\rm{C}}_3 × 5^3 ~+~.~.~.~+~{}^n {\rm{C}}_n × 5^n$
⇒ $6^n-5n~=~1~+~5^2 \left[{}^n {\rm{C}}_2~+~{}^n {\rm{C}}_3 × 5^1 ~+~.~.~.~+~{}^n {\rm{C}}_n × 5^{n-2}\right]$
6. $\left[{}^n {\rm{C}}_2~+~{}^n {\rm{C}}_3 × 5^1 ~+~.~.~.~+~{}^n {\rm{C}}_n × 5^{n-2}\right]$ is a natural number m. So the result in (5) becomes:
6ⁿ - 5n = 1 + 5² × m
⇒ 6ⁿ - 5n = 25m + 1
Hence proved.

---

The link below gives some more solved examples.

Exercise 8.1

---

In the next section we will see some solved examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 8.1 - Binomial Theorem for Any Positive Integer

In the previous section, we saw the basic details about Pascal's triangle. We saw the necessity for developing a rule to find the various numbers in the Pascal's triangle. In this section, we will see such a rule.

The basics about the rule can be written in 6 steps:
1. We have seen the concept of combination in the previous chapter.
We saw the formula: ${}^n {\rm{C}}_r~=~\frac{n!}{r!(n-r)!}$
2. Let us check whether this formula is applicable to the Pascal's triangle. The triangle is shown below for easy reference:

Fig.8.2

The check can be done in 3 steps:
(i) Consider any coefficient in the Pascal's triangle, say the fourth coefficient for index 5
    ♦ The fourth coefficient of index 5 is 10
    ♦ ⁵C₃ is also 10
(ii) Consider any other coefficient in the Pascal's triangle, say the third coefficient for index 7
    ♦ The third coefficient of index 7 is 21
    ♦ ⁷C₂ is also 21
(iii) Let us check one more coefficient in the Pascal's triangle, say the fifth coefficient for index 8
    ♦ The fifth coefficient of index 8 is 70
    ♦ ⁸C₄ is also 70
3. This gives us an idea to pick out any coefficient in the Pascal’s triangle:
The x^th coefficient for any index n will be ⁿC_x-1
• For example, let n be 6 and x be 5
   ♦ Then the 5^th coefficient of index 6 will be be ⁶C_5-1 = ⁶C₄ = 15
   ♦ From the Pascal's triangle, we see that, this is true.
4. Based on this information, the Pascal’s triangle can be modified as shown in fig.8.3 below:

Fig.8.3

• In the modified triangle, we see two points:
(i) In any row, the subscript on the right side of ‘C’ progressively increases in the order: 0, 1, 2, 3, . . . n
   ♦ Where n is the index of that row.
(ii) In any row, the superscript on the left side of ‘C’ does not change.
   ♦ It is equal to n, the index of the row.
5. The above two points give us an idea to quickly write any row of the Pascal’s triangle.
• For example, based on the two points, the row for index 12 will be:
¹²C₀, ¹²C₁, ¹²C₂, ¹²C₃, ¹²C₄, ¹²C₅, ¹²C₆, ¹²C₇, ¹²C₈, ¹²C₉, ¹²C₁₀, ¹²C₁₁, ¹²C₁₂
6. If we can write any row of the Pascal’s triangle quickly, we will be able to write the expansion corresponding to that index also quickly.
• Let us see an example:
Expand (a+b)⁷
Solution:
1. The coefficients will be:
⁷C₀, ⁷C₁, ⁷C₂, ⁷C₃, ⁷C₄, ⁷C₅, ⁷C₆, and ⁷C₇
2. So the expansion will be:
(a+b)⁷ =
⁷C₀ a⁷ + ⁷C₁ a⁶b¹ + ⁷C₂ a⁵b² + ⁷C₃ a⁴b³ + ⁷C₄ a³b⁴ + ⁷C₅ a²b⁵ + ⁷C₆ a¹b⁶  + ⁷C₇ b⁷
• Remember that, the indices of a and b are calculated using the three peculiarities that we wrote in the previous section. They are given below for easy reference:

(i) The total number of terms in the expansion, is one more than the index. (ii) Powers of the first quantity ‘a’ go on decreasing by 1 whereas the powers of the second quantity ‘b’ increase by 1, in the successive terms. (iii) In each term of the expansion, the sum of the indices of a and b is the same and is equal to the index of (a+b).

• Thus we can write the complete expansion.

---

Now we can write the general form. It can be written in 3 steps:
(i) All the coefficients are of the form ⁿC_r
   ♦ For any particular problem, ‘n’ will be a constant.
         ✰ It will be equal to the index in the question.
   ♦ r will increase from 0 to n
(ii) The indices of a and b are calculated using the three peculiarities that we wrote in the previous section (also shown in the box above).
(iii) Based on this, the general form will be:
$(a+b)^n~=~{}^n {\rm{C}}_0 a^n~+~{}^n {\rm{C}}_1 a^{n-1} b~+~{}^n {\rm{C}}_2 a^{n-2} b^2~+~{}^n {\rm{C}}_3 a^{n-3} b^3~+~.~.~.~+~{}^n {\rm{C}}_{n-1} a b^{n-1}~+~{}^n {\rm{C}}_n b^n$

---

• Let us use this general form to expand (2x+5)⁶
We get:

(2x+5)⁶
$\begin{array}{ll} {}={}&{}^6 {\rm{C}}_0 (2x)^6\,5^0 &{}+{}& {}^6 {\rm{C}}_1 (2x)^5\,5^1 &{}+{}& {}^6 {\rm{C}}_2 (2x)^4\,5^2 &{}+{}& {}^6 {\rm{C}}_3 (2x)^3\,5^3 &{}+{}& {}^6 {\rm{C}}_4 (2x)^2\,5^4 &{}+{}& {}^6 {\rm{C}}_5 (2x)^1\,5^5 &{}+{}& {}^6 {\rm{C}}_6 (2x)^0\,5^6 \\ {}={}&{}^6 {\rm{C}}_0 2^6\,x^6\,5^0 &{}+{}& {}^6 {\rm{C}}_1 2^5\,x^5\,5^1 &{}+{}& {}^6 {\rm{C}}_2 2^4\,x^4\,5^2 &{}+{}& {}^6 {\rm{C}}_3 2^3\,x^3\,5^3 &{}+{}& {}^6 {\rm{C}}_4 2^2\,x^2\,5^4 &{}+{}& {}^6 {\rm{C}}_5 2^1\,x^1\,5^5 &{}+{}& {}^6 {\rm{C}}_6 2^0\,x^0\,5^6 \\ {}={}&{}^6 {\rm{C}}_0  × 64 × x^6 × 5^0 &{}+{}& {}^6 {\rm{C}}_1  × 32 × x^5 × 5^1 &{}+{}& {}^6 {\rm{C}}_2  × 16 × x^4\,5^2 &{}+{}& {}^6 {\rm{C}}_3  × 8 × x^3 × 5^3 &{}+{}& {}^6 {\rm{C}}_4  × 4 × x^2 × 5^4 &{}+{}& {}^6 {\rm{C}}_5  × 2 × x^1\,5^5 &{}+{}& {}^6 {\rm{C}}_6  × 1 × x^0\,5^6 \\ {}={}&1  × 64 × x^6 × 5^0 &{}+{}& 6  × 32 × x^5 × 5^1 &{}+{}& 15  × 16 × x^4 × 5^2 &{}+{}& 20  × 8 × x^3 × 5^3 &{}+{}& 15  × 4 × x^2 × 5^4 &{}+{}& 6  × 2 × x^1 × 5^5 &{}+{}& 1  × 1 × x^0 × 5^6 \\ {}={}&1  × 64 × x^6 × 1 &{}+{}& 6  × 32 × x^5 × 5 &{}+{}& 15  × 16 × x^4 × 25 &{}+{}& 20  × 8 × x^3 × 125 &{}+{}& 15  × 4 × x^2 × 625 &{}+{}& 6  × 2 × x^1 × 3125 &{}+{}& 1  × 1 × x^0 × 15625 \\ {}={}&64 x^6 &{}+{}& 960 x^5 &{}+{}& 6000 x^4 &{}+{}& 20000 x^3 &{}+{}& 37500 x^2 &{}+{}& 37500 x &{}+{}& 15625 \\ \end{array}$

---

We have seen the general form. The RHS of that general form is a bit lengthy. It can be easily shortened as explained by the 4 steps below:

1. We see that, the RHS is a sum of a finite number of terms. So it is a summation.
• We can use the symbol '∑' (Greek upper case letter sigma) to denote summation. Thus the general form becomes:
$(a+b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;a^{n-k}\;b^k}$
2. We know that, for any particular problem, n will be a constant. It is the index.
3. k is not a constant. It takes different values in different terms.
• 'k=0' at the bottom of '∑' indicates that, the value of k starts from zero. In other words, the value of k in the first term is zero.
• 'k=n' at the top of '∑' indicates that, the value of k ends at n. In other words, the value of k in the last term is n.
• So the values of k are: 0, 1, 2, 3, . . . n
• It is known as the summation from k = 0 to k = n.
4. The index of a is (n-k). The index of b is k.
This shows that, the sum of the indices of a and b will be n in every term.

---

Let us see some special cases:
Case 1:
In this case, we investigate the expansion when the second quantity is -ve. This can be written in 3 steps:
1. Let us put a = x and b = -y. Then we get:
(a+b)ⁿ = (x-y)ⁿ = [x + (-y)]ⁿ
2. Expanding this using the general form, we get:
$[x+(-y)]^n$
$\begin{array}{ll} {}={}&{}^n {\rm{C}}_0 \,x^n\,(-y)^0 &{}+{}& {}^n {\rm{C}}_1\, x^{n-1}\,(-y)^1 &{}+{}& {}^n {\rm{C}}_2 \,x^{n-2}\,(-y)^2 &{}+{}& {}^n {\rm{C}}_3\, x^{n-3}\,(-y)^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, x^0\,(-y)^n&{}& {} &{} \\ {}={}&{}^n {\rm{C}}_0 \,x^n\,(-1)^0\,y^0 &{}+{}& {}^n {\rm{C}}_1\, x^{n-1}\,(-1)^1\,y^1 &{}+{}& {}^n {\rm{C}}_2 \,x^{n-2}\,(-1)^2\,y^2 &{}+{}& {}^n {\rm{C}}_3\, x^{n-3}\,(-1)^3\,y^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, x^0\,(-1)^n\,y^n&{}& {} &{} \\ \end{array}$
$~{}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, x^{n-k}\;y^k}$
3. Based on the above result, we can write:
$(a-b)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, a^{n-k}\;b^k}$

◼ Let us expand (x-2y)⁵ using this result. We get:
$(x-2y)^5~=~[x+(-2y)]^5~=~\sum\limits_{k\,=\,0}^{k\,=\,5}{{}^5 {\rm{C}}_k\;(-1)^k \, x^{6-k}\;(-2y)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(x-2y)^5$
$\begin{array}{ll} {}={}&{}^5 {\rm{C}}_0 \,x^5\,(-1)^0\,(2y)^0 &{}+{}& {}^5 {\rm{C}}_1\, x^{5-1}\,(-1)^1\,(2y)^1 &{}+{}& {}^5 {\rm{C}}_2 \,x^{5-2}\,(-1)^2\,(2y)^2 &{}+{}& {}^5 {\rm{C}}_3\, x^{5-3}\,(-1)^3\,(2y)^3 &{}+{}& {}^5 {\rm{C}}_4\, x^{5-4}\,(-1)^4\,(2y)^4 &{}+{}& {}^5 {\rm{C}}_5\, x^{5-5}\,(-1)^5\,(2y)^5&{}& {} &{} \\ {}={}&1 × x^5 × 1 × (2y)^0 &{}+{}& 5 × x^4 × -1 × (2y) &{}+{}& 10 × x^3 × 1 × (4y^2) &{}+{}& 10 × x^2 × -1 × (8y^3) &{}+{}& 5 × x^1 × 1 × (16y^4) &{}+{}& 1 × x^0 × -1 × (32y^5) \\ {}={}&x^5 &{}-{}& 10x^4 y &{}+{}& 40x^3 y^2 &{}-{}& 80 x^2 y^3 &{}+{}& 80 x y^4 &{}-{}& 32y^5 \\ \end{array}$

---

Case 2:
In this case, we investigate the expansion when the first quantity is 1. This can be written in 3 steps:
1. Let us put a = 1 and b = x. Then we get:
(a+b)ⁿ = (1+x)ⁿ
2. Expanding this using the general form, we get:
$(1+x)^n$
$\begin{array}{ll} {}={}&{}^n {\rm{C}}_0 \,1^n\,x^0 &{}+{}& {}^n {\rm{C}}_1\, 1^{n-1}\,x^1 &{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,x^2 &{}+{}& {}^n {\rm{C}}_3\, 1^{n-3}\,x^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,x^n&{}& {} &{} \\ {}={}&{}^n {\rm{C}}_0 \,1^n\,x^0 &{}+{}& {}^n {\rm{C}}_1\, 1^{n-1}\,x^1 &{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,x^2 &{}+{}& {}^n {\rm{C}}_3\, 1^{n-3}\,x^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,x^n&{}& {} &{} \\ \end{array}$
${}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\, 1^{n-k}\;x^k}$
3. So we can write:
$(1+x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;x^k}$
◼ Let us expand (1+2x)⁶ using this result. We get:
$(1+2x)^6~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^6 {\rm{C}}_k\;(2x)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(1+2x)^6$
$\begin{array}{ll} {}={}&{}^6 {\rm{C}}_0 \,1^6\,(2x)^0 &{}+{}& {}^6 {\rm{C}}_1\,(2x)^1 &{}+{}& {}^6 {\rm{C}}_2\,(2x)^2 &{}+{}& {}^6 {\rm{C}}_3\,(2x)^3 &{}+{}& {}^6 {\rm{C}}_4\,(2x)^4 &{}+{}& {}^6 {\rm{C}}_5\,(2x)^5 &{}+{}& {}^6 {\rm{C}}_6\,(2x)^6&{}& {} &{} \\ {}={}&1 × (2x)^0 &{}+{}& 6 × (2x) &{}+{}& 15 × (4x^2) &{}+{}& 20 × (8x^3) &{}+{}& 15 × (16x^4) &{}+{}& 6 × (32x^5) &{}+{}& 1 × (64x^6) \\ {}={}&1 &{}+{}& 12x &{}+{}& 60 x^2 &{}+{}& 160 x^3 &{}+{}& 240 x^4 &{}+{}& 192 x^5 &{}+{}& 64x^6 \\ \end{array}$

◼ x = 1 is a special case coming under this category. We get:
$(1+x)^n~=~(1+1)^n~=~2^n~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k\;x^k}~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k\;1^k}~=~\sum\limits_{k\,=\,0}^{k\,=\,6}{{}^n {\rm{C}}_k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
${}={}~{}^n {\rm{C}}_0 ~+~{}^n {\rm{C}}_1 ~+~{}^n {\rm{C}}_2 ~+~{}^n {\rm{C}}_3 ~+~.~.~.~+~{}^n {\rm{C}}_n$
• So we can write:
$2^n~=~{}^n {\rm{C}}_0 ~+~{}^n {\rm{C}}_1 ~+~{}^n {\rm{C}}_2 ~+~{}^n {\rm{C}}_3 ~+~.~.~.~+~{}^n {\rm{C}}_n$  

---

Case 3:
In this case, we investigate the expansion when the first quantity is 1 and the second quantity is -ve. This can be written in 3 steps:
1. Let us put a = 1 and b = -x. Then we get:
(a+b)ⁿ = (1-x)ⁿ = [1 + (-x)]ⁿ
2. Expanding this using the general form, we get:
$[1+(-x)]^n$
$\begin{array}{ll} {}={}&{}^n {\rm{C}}_0 \,1^n\,(-x)^0 &{}+{}& {}^n {\rm{C}}_1\, 1^{n-1}\,(-x)^1 &{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,(-x)^2 &{}+{}& {}^n {\rm{C}}_3\, 1^{n-3}\,(-x)^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,(-x)^n&{}& {} &{} \\ {}={}&{}^n {\rm{C}}_0 \,1^n\,(-1)^0\,x^0 &{}+{}& {}^n {\rm{C}}_1\, 1^{n-1}\,(-1)^1\,x^1 &{}+{}& {}^n {\rm{C}}_2 \,1^{n-2}\,(-1)^2\,x^2 &{}+{}& {}^n {\rm{C}}_3\, 1^{n-3}\,(-1)^3\,x^3 &{}+{}& .~.~.~+~{}^n {\rm{C}}_n\, 1^0\,(-1)^n\,x^n&{}& {} &{} \\ \end{array}$
${}={}~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \, 1^{n-k}\;x^k}$
3. Based on the above result, we can write:
$(1-x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;x^k}$

◼ Let us expand (1-2x)⁵ using this result. We get:
$(1-2x)^5~=~[1+(-2x)]^5~=~\sum\limits_{k\,=\,0}^{k\,=\,5}{{}^5 {\rm{C}}_k\;(-1)^k\;(-2x)^k}$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
$(1-2x)^5$
$\begin{array}{ll} {}={}&{}^5 {\rm{C}}_0\,(-1)^0\,(2x)^0 &{}+{}& {}^5 {\rm{C}}_1\,(-1)^1\,(2x)^1 &{}+{}& {}^5 {\rm{C}}_2\,(-1)^2\,(2x)^2 &{}+{}& {}^5 {\rm{C}}_3\,(-1)^3\,(2x)^3 &{}+{}& {}^5 {\rm{C}}_4\,(-1)^4\,(2x)^4 &{}+{}& {}^5 {\rm{C}}_5\,(-1)^5\,(2x)^5&{}& {} &{} \\ {}={}&1 × 1 × (2x)^0 &{}+{}& 5 × -1 × (2x) &{}+{}& 10 × 1 × (4x^2) &{}+{}& 10 × -1 × (8x^3) &{}+{}& 5 × 1 × (16x^4) &{}+{}& 1 × -1 × (32x^5) \\ {}={}&1 &{}-{}& 10 x &{}+{}& 40 x^2 &{}-{}& 80 x^3 &{}+{}& 80 x^4 &{}-{}& 32 x^5 \\ \end{array}$

• We wrote: $(1-x)^n~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;x^k}$
◼ x = 1 is a special case coming under this category. We get:
$(1-x)^n~=~(1-1)^n~=~0^n ~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k \;1^k} ~=~\sum\limits_{k\,=\,0}^{k\,=\,n}{{}^n {\rm{C}}_k\;(-1)^k }$
• Once we write the sigma notation on the RHS, we will be able to write all the terms easily. We get:
${}={}~{}^n {\rm{C}}_0\;(-1)^0 ~+~{}^n {\rm{C}}_1\;(-1)^1 ~+~{}^n {\rm{C}}_2\;(-1)^2 ~+~{}^n {\rm{C}}_3 ~+~.~.~.~+~{}^n {\rm{C}}_n\;(-1)^n$
• So we can write:
$0^n~=~{}^n {\rm{C}}_0 ~-~{}^n {\rm{C}}_1 ~+~{}^n {\rm{C}}_2 ~-~{}^n {\rm{C}}_3 ~+~.~.~.~+~(-1)^n~ × ~{}^n {\rm{C}}_n$

---

In the next section we will see some solved examples.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 7.7 - Miscellaneous Examples

In the previous section, we completed a discussion on combinations. We saw some solved examples also. In this section we will see some miscellaneous examples.

Solved example 7.21
How many words, with or without meaning, each of 3 vowels and 2 consonants can be formed from the letters of the word INVOLUTE ?
Solution:
1. The word INVOLUTE has,
    ♦ 4 vowels: I, O, U, E
    ♦ 4 consonants: N, V, L, T
2. Each word must have 3 vowels and 2 consonants. That means, each word will have 5 letters. So let there be 5 boxes.
    ♦ The first 3 boxes can be considered as one unit.
    ♦ The remaining two boxes can be considered as another unit.
• This is shown in the fig.7.10 below:

Fig.7.10

3. The first unit is for vowels.
• There are 4 vowels. So this unit can be filled in in ⁴C₃ ways.
4. The remaining unit is for consonants.
• There are 4 consonants. So this unit can be filled in in ⁴C₂ ways.
5. So by applying the multiplication principle, the two units can be filled in:
⁴C₃ × ⁴C₂ ways
6. Consider the following two arrangements:
    ♦ IOUNV
    ♦ IUONV
• These are two different permutations of the letters I, U, O, N, V.
    ♦ But same combination of those letters.
    ♦ Different combinations will be counted only once
    ♦ So in this problem, we want no. of permutations, not no. of combinations
7. So we must modify the result obtained in (5). It can be done in 2 steps:
(i) In each of the ⁴C₃ × ⁴C₂ combinations, the five letters can be arranged in 5! ways.
(ii) So the number of permutations = ⁴C₃ × ⁴C₂ × 5! = 2880 ways

Solved example 7.22
A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has (i) no girl ? (ii) at least one boy and one girl ?
(iii) at least 3 girls ?
Solution:
◼ This is not a permutation problem. It is a combination problem. Each arrangement should contain the specified numbers. The order is not important.
Part (i):
1. Let there be 5 boxes.
All those 5 boxes should be filled with B. None of those boxes must contain G
2. That means, we must use only the seven boys.
5 boys can be selected from 7 boys in ⁷C₅ = 21 ways.

Part (ii):
1. At least one boy and one girl can be selected in the following ways:
(a) 1 boy and 4 girls
(b) 2 boys and 3 girls
(c) 3 boys and 2 girls
(d) 4 boys and 1 girl
2. Consider the arrangement in (a)
   ♦ 1 boy can be selected from 7 boys in ⁷C₁ ways.
   ♦ 4 girls can be selected from 4 girls in ⁴C₄ ways.
• So 1 boy and 4 girls can be selected in ⁷C₁ × ⁴C₄ = 7 ways.
3. Consider the arrangement in (b)
   ♦ 2 boys can be selected from 7 boys in ⁷C₂ ways.
   ♦ 3 girls can be selected from 4 girls in ⁴C₃ ways.
• So 2 boys and 3 girls can be selected in ⁷C₂ × ⁴C₃ = 84 ways.
4. Consider the arrangement in (c)
   ♦ 3 boys can be selected from 7 boys in ⁷C₃ ways.
   ♦ 2 girls can be selected from 4 girls in ⁴C₂ ways.
• So 3 boys and 2 girls can be selected in ⁷C₃ × ⁴C₂ = 210 ways.
5. Consider the arrangement in (d)
   ♦ 4 boys can be selected from 7 boys in ⁷C₄ ways.
   ♦ 1 girl can be selected from 4 girls in ⁴C₁ ways.
• So 4 boys and 1 girl can be selected in ⁷C₄ × ⁴C₁ = 140 ways.
6. So total number of ways for selecting at least one boy and one girl is:
(7 + 84 + 210 +140) = 441 ways.

Part (iii):
1. At least 3 girls can be selected in the following ways:
(a) 3 girls and 2 boys
(b) 4 girls and 1 boy
(more than 4 girls is not possible because, the maximum number of girls in the given group is 4)
2. Consider the arrangement in (a)
   ♦ 3 girls can be selected from 4 girls in ⁴C₃ ways.
   ♦ 2 boys can be selected from 7 boys in ⁷C₂ ways.
• So 3 girls and 2 boys can be selected in ⁴C₃ × ⁷C₂ = 84 ways.
3. Consider the arrangement in (b)
   ♦ 4 girls can be selected from 4 girls in ⁴C₄ ways.
   ♦ 1 boy can be selected from 7 boys in ⁷C₁ ways.
• So 4 girls and 1 boy can be selected in ⁴C₄ × ⁷C₁ = 7 ways.
4. So total number of ways for selecting at least three girls is:
(84 + 7) = 91 ways.

Solved example 7.23
Find the number of words with or without meaning which can be made using all the letters of the word AGAIN. If these words are written as in a dictionary, what will be the 50^th word?
Solution:
◼ This is a permutation problem. The order is important. Each order will give a different word.
Part (i):
• There are 5 letters in the word AGAIN. The letter A appears twice.
• So the number of words = $\frac{5!}{2!}$ = 60

Part (ii):
1. Let us find the number of words beginning with A:
(i) Let there be 5 boxes.
(ii) The first box is fixed with A
(iii) The remaining 4 boxes can be filled in 4! ways.
(iv) So the number of words beginning with A = (1 × 4!) = 24
2. In the word AGAIN, the letter coming after A in the alphabetical order is G.
• Let us find the number of words beginning with G:
(i) Let there be 5 boxes.
(ii) The first box is fixed with G
(iii) The remaining 4 boxes can be filled in $\frac{4!}{2!}$ = 12 ways.
(iv) So the number of words beginning with G = (1 × 4!) = 12 
3. In the word AGAIN, the letter coming after G in the alphabetical order is I.
• Let us find the number of words beginning with I:
(i) Let there be 5 boxes.
(ii) The first box is fixed with I
(iii) The remaining 4 boxes can be filled in $\frac{4!}{2!}$ = 12 ways.
(iv) So the number of words beginning with I = (1 × 4!) = 12
4. From the above steps, we get:
Number of words beginning with A, G and I = (24+12+12) =48
5. In the word AGAIN, the letter coming after I in the alphabetical order is N.
• So the 49^th word will begin with N.
6. The letters after N in the alphabetical order are: A, A, G, I
• So the 49^th word is NAAGI
7. The next alphabetical order is: N, A, A, I, G
• So the 50^th word is NAAIG

Solved example 7.24
How many numbers greater than 1000000 can be formed by using the digits 1, 2, 0, 2, 4, 2, 4?
Solution:
◼ This is a permutation problem. The order is important. Each order will give a different number.
1. There are seven digits in the given number 1000000.
• So we must use all the given seven digits to form numbers. Then only we will get numbers greater than 1000000
2. Among the given digits, ‘2’ is present three times. Also ‘4’ is present two times.
• So the number of seven digit numbers = $\frac{7!}{(3!)(2!)}$ = 420
3. Out of these numbers, some will be beginning with ‘0’
• Number of numbers beginning with ‘0’ is: $\frac{6!}{(3!)(2!)}$ = 60
4. So the actual number of numbers greater than 1000000 is:
(420 - 60) = 360

Solved example 7.25
In how many ways can 5 girls and 3 boys be seated in a row so that no two boys are together?
Solution:
◼ This is a permutation problem. The order is important. Each order will give a different arrangement.
1. Consider the following arrangement:
XGXGXGXGXGX
2. Boys can be seated at any of the 'X' marks.
• There are six 'X' marks. So there are six seats available for boys.
• Three boys can sit in six seats in ⁶P₃ = 120 ways.
3. Five girls can be seated in 5! = 120 ways.
4. So the required arrangement can be achieved in (120 × 120) = 14400 ways

---

The link below gives some more solved examples:

Miscellaneous Exercise on chapter 7

---

We have completed a discussion on permutations and combinations. In the next chapter, we will see Binomial theorem.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com

Chapter 8 - Binomial Theorem

In the previous section, we completed a discussion on permutations and combinations. In this chapter, we will see Binomial theorem.

Some basics can be written in 4 steps:
1. In our earlier classes, we have seen the basics about polynomials (Details here and here).
• Now, a binomial is a polynomial having two terms.
   ♦ In some binomials the two terms will be added together.
   ♦ In some binomials, one term will be subtracted from the other term.
• Some examples of binomials are: (a+b), (a-b), (2x²-3), (4x+5) etc.,
2. In many scientific and engineering problems, we will want to find squares, cubes and higher powers of binomials. Let us see some examples:
(i) (4x+5)² is the square of the binomial (4x+5)
   ♦ It can be easily calculated using the identity: (a+b)² = a²+2ab+b²
• Here, the binomial is raised to the power 2
• Power is also known as index (plural indices)
(ii) (4x+5)³ is the cube of the binomial (4x+5)
   ♦ It can be easily calculated using the identity: (a+b)³ = a³+3a²b+3ab²+b³
• Here, the binomial is raised to the power 3
(iii) When the binomial (4x+5) is raised to the power 4, we write: (4x+5)⁴
   ♦ It can be calculated using the identity:
(a+b)⁴ = (a+b)(a+b)³ = (a+b)(a³+3a²b+3ab²+b³) = a⁴+4a³b+6a²b²+4ab³+b⁴
• Here, the binomial is raised to the power 4
(iv) When the binomial is raised to the power 5, we write: (4x+5)⁵
so on . . .
• From the 5^th power on wards, the calculations become lengthy.
3. In general, when a binomial is raised to the power n, we write  (a+b)ⁿ
   ♦ n can be an integer like -3, 2, -5 etc.,
   ♦ n can be a rational number like $-\frac{1}{3},~\frac{2}{5}$ etc.,
4. We will encounter situations where,
   ♦ n is very large like 12, 25, -14 etc.,
   ♦ n is rational numbers like $-\frac{1}{3},~\frac{2}{5}$ etc.,
◼ In such cases, the binomial theorem helps us to reduce calculation steps.
• In this chapter we will see how binomial theorem helps us when n is a +ve integer.
• In higher classes, we will see the cases where n is -ve integer or rational number.

---

Pascal's Triangle

Binomial theorem is based on Pascal's Triangle. It's details can be written in 3 steps:
1. Consider the basic identities:
   ♦ When n = 0, (a+b)ⁿ = (a+b)⁰ = 1 [Here (a+b) should not be equal to zero]
   ♦ When n = 1, (a+b)ⁿ = (a+b)¹ = (a+b)    
   ♦ When n = 2, (a+b)ⁿ = (a+b)² = a²+2ab+b²
   ♦ When n = 3, (a+b)ⁿ = (a+b)³ = a³+3a²b+3ab²+b³
   ♦ When n = 4, (a+b)ⁿ = (a+b)⁴ = a⁴+4a³b+6a²b²+4ab³+b⁴
2. In the above expansions, we see three peculiarities:
(i) The total number of terms in the expansion, is one more than the index.
• For example, consider (a+b)³:
The index is 3 and the number of terms in the expansion is 4
(ii) Powers of the first quantity ‘a’ go on decreasing by 1 whereas the powers of the
second quantity ‘b’ increase by 1, in the successive terms.
• For example, consider (a+b)⁴ = a⁴+4a³b+6a²b²+4ab³+b⁴ :
   ♦ In the first term, power of a is 4 and that of b is 0
   ♦ In the second term,
         ✰ the power of a decreases by 1 and becomes 3
         ✰ the power of b increases by 1 and becomes 1
   ♦ In the third term,
         ✰ the power of a decreases by 1 and becomes 2
         ✰ the power of b increases by 1 and becomes 2
   ♦ In the fourth term,
         ✰ the power of a decreases by 1 and becomes 1
         ✰ the power of b increases by 1 and becomes 3
   ♦ In the fifth term,
         ✰ the power of a decreases by 1 and becomes 0
         ✰ the power of b increases by 1 and becomes 4
(iii) In each term of the expansion, the sum of the indices of a and b is the same and is equal to the index of (a+b).
• For example, consider (a+b)⁴ = a⁴+4a³b+6a²b²+4ab³+b⁴ :
   ♦ In the first term, the sum of the indices is (4+0) = 4
         ✰ Sum is same as the index of (a+b)⁴.
   ♦ In the second term, the sum of the indices is (3+1) = 4
         ✰ Sum is same as the index of (a+b)⁴.
   ♦ In the third term, the sum of the indices is (2+2) = 4
         ✰ Sum is same as the index of (a+b)⁴.
   ♦ In the fourth term, the sum of the indices is (1+3) = 4
         ✰ Sum is same as the index of (a+b)⁴.
   ♦ In the fifth term, the sum of the indices is (0+4) = 4
         ✰ Sum is same as the index of (a+b)⁴.
3. Now we will see an interesting relation between the coefficients of the expansions. It can be written in 4 steps:
(i) Fig.8.1 below shows the coefficients written in order.
• The first row shows the coefficients when (a+b) is raised to the power zero.
   ♦ We know that, any number raised to zero will give 1.
   ♦ So there is a one in the first row.

Fig.8.1

• The second row shows the coefficients when (a+b) is raised to the power 1.
   ♦ We know that, (a+b) raised to 1 will give the same (a+b).
         ✰ Coefficient of the first term is 1.
         ✰ Coefficient of the second term is 1.
   ♦ Thus there are two ones in the second row.
• The third row shows the coefficients when (a+b) is raised to the power 2.
   ♦ We know that, (a+b) raised to 2 will give a²+2ab+b².
         ✰ Coefficient of the first term is 1.
         ✰ Coefficient of the second term is 2.
         ✰ Coefficient of the third term is 1.
   ♦ Thus in the third row, we have 1, 2, 1
• The fourth row shows the coefficients when (a+b) is raised to the power 3.
   ♦ We know that, (a+b) raised to 3 will give a³+3a²b+3ab²+b³.
         ✰ Coefficient of the first term is 1.
         ✰ Coefficient of the second term is 3.
         ✰ Coefficient of the third term is 3.
         ✰ Coefficient of the fourth term is 1.
   ♦ Thus in the fourth row, we have 1, 3, 3, 1
• The fifth row shows the coefficients when (a+b) is raised to the power 4.
   ♦ We know that, (a+b) raised to 4 will give a⁴+4a³b+6a²b²+4ab³+b⁴.
         ✰ Coefficient of the first term is 1.
         ✰ Coefficient of the second term is 4.
         ✰ Coefficient of the third term is 6.
         ✰ Coefficient of the fourth term is 4.
         ✰ Coefficient of the fifth term is 1.
   ♦ Thus in the fifth row, we have 1, 4, 6, 4, 1
(ii) We can easily write the coefficients up to the row where the index is 4.
    ♦ For writing the next row, we first will need to expand (a+b)⁵
    ♦ For writing the row below that, we will first need to expand (a+b)⁶.
    ♦ So on . . .
(iii) This is a lengthy process. So we must find an easier way.
◼ In fig.8.1, we see a pattern:
    ♦ Adding the two ones in index 1, will give the middle coefficient in index 2.
    ♦ This is indicated by the top most triple headed arrow in fig.8.2 below:

Fig.8.2

• Similarly,
    ♦ Adding 1 and 2 of index 2 will give the first 3 in index 3
    ♦ Adding 2 and 1 of index 2 will give the second 3 in index 3
    ♦ This is indicated by the two triple headed arrows in the third row (row for index 2).
• We can continue like this and find the coefficients for higher indices.
(iv) The structure in fig.8.2 looks like a triangle.
    ♦ At the apex of the triangle, there is a ‘1’
    ♦ Along the left sloping side side of the triangle, all numbers are ‘1’
    ♦ Along the right sloping side of the triangle, all numbers are ‘1’
• This array of numbers is known as Pascal’s triangle. This name is given in honor of the French Mathematician Blaise Pascal.

---

Let us see an example:
Expand (2x+3y)⁵ using Pascal’s triangle
Solution:
1. Based on the peculiarities that we wrote in step (2) above,
    ♦ In the first term, the first quantity (2x) will have a power of 5
    ♦ In the first term, the second quantity (3y) will have a power of 0
• Using the Pascal's triangle in fig.8.2, we get:
    ♦ In the first term, the coefficient will be '1'
• Combining these three information, we get:
First term = 1 × (2x)⁵ × (3y)⁰ = 32x⁵
2. Based on the peculiarities that we wrote in step (2) above,
    ♦ In the second term, the first quantity (2x) will have a power of 4
    ♦ In the second term, the second quantity (3y) will have a power of 1
• Using the Pascal's triangle in fig.8.2, we get:
    ♦ In the second term, the coefficient will be '5'
• Combining these three information, we get:
Second term = 5 × (2x)⁴ × (3y)¹ = 240x⁴y
3. Based on the peculiarities that we wrote in step (2) above,
    ♦ In the third term, the first quantity (2x) will have a power of 3
    ♦ In the third term, the second quantity (3y) will have a power of 2
• Using the Pascal's triangle in fig.8.2, we get:
    ♦ In the third term, the coefficient will be '10'
• Combining these three information, we get:
Third term = 10 × (2x)³ × (3y)² = 720x³y²
4. In this way, we can write all the terms. We get:
(2x+3y)⁵ = 32x⁵ + 240x⁴y + 720x³y² + 1080x²y³+ 810xy⁴+ 243y⁵

---

• We have successfully written the expansion of (2x+3y)⁵.
• What if we want the expansion of (2x+3y)¹² ?
    ♦ We will have to write all the rows of the Pascal's triangle up to index 12.
    ♦ This is a lengthy process.
• So we must develop a rule that will help us to write any row in the Pascal's triangle, with out writing the rows above it.
• We will see such a rule in the next section.

Previous

Contents

Next

Copyright©2022 Higher secondary mathematics.blogspot.com