In the previous section, we completed a discussion on derivatives of inverse trigonometric functions. In this section, we will see exponential functions.
First we will see some basics about polynomial functions. It can be written in 4 steps:
1.Consider the following five polynomial functions:
(i) y = f1(x) = x1
(ii) y = f2(x) = x2
(iii) y = f3(x) = x3
(iv) y = f4(x) = x4
(v) y = f5(x) = x5
•
They have the general form y = fn(x) = xn
2. Fig.21.15 below shows the graphs of these functions.
 |
| Fig.21.15 |
•
We see that, as n increases, the curves become steeper.
♦ "Steeper" means, the graph leans more towards the y-axis.
♦ "Flatter" means, the graph leans more towards the x-axis.
3. For a steeper curve, growth will be faster. That is., even for a small increase in x, there will be a large increase in y.
•
This can be demonstrated by comparing two graphs. The comparison can be written in (v) steps:
(i) Let us compare the graphs of
♦ y = f10(x) = x10 and
♦ y = f15(x) = x15
•
15 > 10. So y = f15(x) = x15 will be steeper than y = f10(x) = x10.
(ii) Consider y = f10(x) = x10.
•
Beginning from x = 2, let us move a distance of 3 units along the x axis, towards the right.
•
So we begin from x = 2 and end at x = 5.
♦ At x = 2, y = 210.
♦ At x = 5, y = 510.
•
The corresponding increase in y is:
(510 − 210) = (9765625 − 1024) = 9764601
(iii) Consider y = f15(x) = x15.
•
Let us move the same distance, from the same point, in the same direction.
•
So we begin from x = 2 and end at x = 5.
♦ At x = 2, y = 215.
♦ At x = 5, y = 515.
•
The corresponding increase in y is:
(515 − 215) = (30517578125 − 32768) = 30517545357.
(iv) Comparing 9764601 and 30517545357, we can write:
•
For the same increase in x,
♦ y = f15(x) = x15
♦ gives a greater increase in y than
♦ y = f10(x) = x10.
(v) So we can conclude that:
•
For the same increase in x,
♦ the steeper curve
♦ gives a greater increase in y than
♦ the flatter curve.
4. Based on the above comparison, we can write:
Rate of growth of a polynomial function is dependent on the degree of that polynomial function. Higher the degree, higher is the rate of growth. We will see the actual proof in higher classes.
•
Consider a polynomial function with a very large degree. Even such a large degree will not be sufficient to describe some situations in science and engineering. Loudness of sound, radioactive decay, wave lengths in electromagnetic spectrum, are examples.
•
In such situations, we use exponential functions.
•
Exponential functions have the general form: y = f(x) = bx.
♦ where b > 0 and b ≠ 1.
♦ As a sample, y = f(x) = 10x is plotted in the fig.21.15 above.
•
Rate of growth of an exponential function, will be greater than that of any polynomial function. This is true when x is very large.
•
This fact can be demonstrated by a simple comparison. It can be written in (v) steps:
(i) Let us compare the graphs of
♦ y = f100(x) = x100 and
♦ y = f(x) = 10x
(ii) Consider y = f100(x) = x100.
•
Let us move from x = 103 to x = 105
♦ At x = 103, y = (103)100 = 10300.
♦ At x = 105, y = (105)100 = 10500.
•
The corresponding increase in y is:
(10500 − 10300)
(iii) Consider y = f(x) = 10x.
•
Let us move the same distance, from the same point, in the same direction.
♦ At x = 103, y = (10)103 = 101000.
♦ At x = 105, y = (10)105 = 10100000.
•
The corresponding increase in y is:
(10100000 − 101000).
(iv) Comparing (10500 − 10300) and (10100000 − 101000), we can write:
•
For the same increase in x,
♦ y = f(x) = 10x
♦ gives a greater increase in y than
♦ y = f100(x) = x100.
(v) So we can conclude that:
•
For the same increase in x,
♦ the exponential function
♦ gives a greater increase in y than
♦ the polynomial function.
Let us write the important features about exponential functions. It can be written in 6 steps:
1. The general form of the exponential function is: f(x) = bx
♦ b should be greater than zero.
♦ b should not be equal to 1.
2. Let us see why b should be greater than zero. It can be written in (iii) steps.
(i) Suppose that, b = −9.
Then the function will be y = f(−9) = (−9)x
(ii) While plotting the graph, when the input is 1/2, we get:
$f_{(-9)} = (-9)^{\frac{1}{2}} = \sqrt{-9} = 3i$
•
This is not defined because, $3i$ is not a real number.
(iii) To avoid such situations, we avoid −ve numbers altogether.
3. Let us see why b should not be equal to one. It can be written in (iii) steps.
(i) Suppose that, b = 1.
Then the function will be y = f1 = 1x
(ii) While plotting the graph, whatever is the input, we will get y = f1(x) = 1
•
This is a constant function. A constant function is not useful for describing variation of quantities like loudness of sound, wavelengths in the electromagnetic spectrum etc,.
(iii) To avoid such a situation, we avoid 1.
4. Fig.21.16 below shows the graphs of some simple exponential functions.
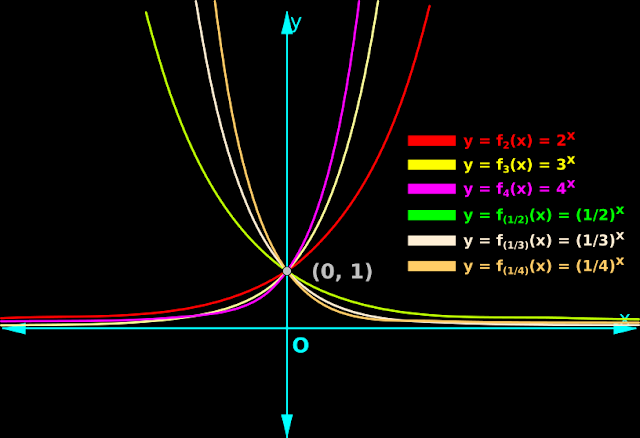 |
| Fig.21.16 |
•
Red, yellow and magenta belong to the category: b > 1
•
Green, pink and orange belong to the category: 0 < b < 1
5. From the graphs, we see that,
•
When b >1:
♦ As x increases towards ∞, f(x) also approaches ∞.
✰ Red, yellow and magenta are rising up.
♦ As x decreases towards −∞, f(x) approaches zero.
✰ Red, yellow and magenta are approaching x-axis.
•
When 0 < b < 1:
♦ As x increases towards ∞, f(x) approaches zero.
✰ Green, pink and orange are approaching x-axis.
♦ As x decreases towards −∞, f(x) approaches ∞.
✰ Green, pink and orange are rising up.
6. From the graphs, we get the following information also:
•
Any real number can be used as an input for exponential function. That means, the domain is (−∞,∞)
•
The output of an exponential function can never be zero. It can only approach zero.
•
The output of an exponential function will be always +ve.
•
The range of an exponential function is (0,∞).
•
For an exponential function, the point (0,1) will be always available. This is because, any number raised to the power zero, is 1.
Now we will see common exponential function. It can be explained in 2 steps:
1. We know that, the general form of exponential function is: f(x) = bx.
•
"b" is called base of the exponential function.
2. If b = 10, then we get: f(x) = 10x.
•
This function is known as common exponential function.
Finally we will see natural exponential function. It can be explained in 5 steps:
1. We know that, the general form of exponential function is: f(x) = bx.
•
"b" is called base of the exponential function.
2. If b = e, then we get: f(x) = ex.
•
This function is known as natural exponential function.
3. Recall that, e is the sum of the infinite series:
$1 + \frac{1}{1!}+ \frac{1}{2!} + ~.~.~.$ (Details here)
•
The value of e is 2.71828182845905…
4. We see that, e lies between 2 and 3. So the graph of the natural exponential function will lie between the graphs of y = f2 = 2x and y = f3 = 3x .
•
It is shown in the fig.21.17 below:
 |
| Fig.21.17 |
5. Many problems in science, engineering and economics give simple solutions if e is used as the base. Instead of e, if 10 is used, those solutions will become large and complicated.
We have completed a discussion on exponential functions. In the next section, we will see logarithmic functions.
Copyright©2024 Higher secondary mathematics.blogspot.com
No comments:
Post a Comment